
【题目】四边形OBCD中的三个顶点在⊙O上,点A是⊙O上的一个动点(不与点B、C、D重合)。若四边形OBCD是平行四边形时,那么![]() 的数量关系是________________.
的数量关系是________________.

【答案】![]() 或
或![]() 或
或![]() 或
或![]()
【解析】连接OC,∵四边形OBCD是平行四边形, OB=OD,∴平行四边形OBCD是菱形,∴OB=BC=CD=OD,∵OC=OB=OD,∴△OBC与△OCD是等边三角形,∴∠BOC=∠BCO=∠DOC=∠DCO=60°,∴∠BOD=∠BCD=120°,
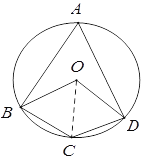
如图1、图3、图4时,∠A=![]() ∠BOD=60°,∴图1中∠OBA+∠ODA=60°,图3中∠OBA-∠ODA=60°,图4中∠ODA-∠OBA=60°;
∠BOD=60°,∴图1中∠OBA+∠ODA=60°,图3中∠OBA-∠ODA=60°,图4中∠ODA-∠OBA=60°;
如图2时,∠A=∠BCD=120°,∴∠OBA+∠ODA=120°.
综上,∠OBA+∠ODA=60°或∠OBA-∠ODA=60°或∠ODA-∠OBA=60°或∠OBA+∠ODA=120°.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将坐标是(0,4),(1,0),(2,4),(3,0),(4,4)的点用线段依次连接起来形成一个图案.
(1)在下列坐标系中画出这个图案;
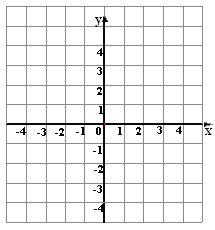
(2)若将上述各点的横坐标保持不变,纵坐标分别乘以-1,再将所得的各个点用线段依次连接起来,所得的图案与原图案相比有什么变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,OC平分∠AOB,点P在OC上,若⊙P与OA相切,那么⊙P与OB位置关系是 .

(2)如图2,⊙O的半径为2,∠AOB=120°,
①若点P是⊙O上的一个动点,当PA=PB时,是否存在⊙Q,同时与射线PA.PB相切且与⊙O相切,如果存在,求出⊙Q的半径; 如果不存在,请说明理由.
②若点P在BO的延长线上,且满足PA⊥PB,是否存在⊙Q,同时与射线PA.PB相切且与⊙O相切,如果存在,请直接写出⊙Q的半径; 如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤PD=![]() EC.其中正确结论的番号是( )
EC.其中正确结论的番号是( )

A.①②④⑤B.①②③④⑤C.①②④D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
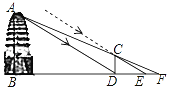
【题目】如图是位于陕西省西安市荐福寺内的小雁塔,是中国早期方形密檐式砖塔的典型作品,并作为丝绸之路的一处重要遗址点,被列入《世界遗产名录》.小铭、小希等几位同学想利用一些测量工具和所学的几何知识测量小雁塔的高度,由于观测点与小雁塔底部间的距离不易测量,因此经过研究需要进行两次测量,于是在阳光下,他们首先利用影长进行测量,方法如下:小铭在小雁塔的影子顶端D处竖直立一根木棒CD,并测得此时木棒的影长DE=2.4米;然后,小希在BD的延长线上找出一点F,使得A、C、F三点在同一直线上,并测得DF=2.5米.已知图中所有点均在同一平面内,木棒高CD=1.72米,AB⊥BF,CD⊥BF,试根据以上测量数据,求小雁塔的高度AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从热气球C处测得地面A,B两点的俯角分别为30°,45°,此时热气球C处所在位置到地面上点A的距离为400米.求地面上A,B两点间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,F为BC的中点,D为CA延长线上一点,∠DFE=∠B.
(1)求证:△CDF∽△BFE;
(2)若EF∥CD,求证:2CF2=ACCD.

查看答案和解析>>
科目:初中数学 来源: 题型:
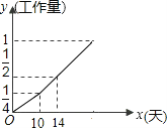
【题目】甲、乙两个工程队完成某项工程,首先是甲队单独做了10天,然后乙队加入合作,完成剩下的全部工程,设工程总量为单位1,工程进度满足如图所示的函数关系.
(1)求甲、乙两队合作完成剩下的全部工程时,工作量y与天数x间的函数关系式;
(2)求实际完成这项工程所用的时间比由甲队单独完成这项工程所需时间少多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且经过点(﹣1,0),下列四个结论:①如果点(![]() ,y1)和(2,y2)都在抛物线上,那么y1<y2;②b2﹣4ac>0;③m(am+b)<a+b(m≠1的实数);④
,y1)和(2,y2)都在抛物线上,那么y1<y2;②b2﹣4ac>0;③m(am+b)<a+b(m≠1的实数);④![]() ;其中正确的有( )
;其中正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com