
【题目】已知关于x的方程x2-2x+a=0有两个不相等的实数根,则a的取值范围为______________.
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】一种面粉的质量标识为“26±0.25千克”,则下列面粉中合格的是:( )
A. 26.30千克 B. 25.70千克 C. 26.51千克 D. 25.80千克
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1﹣x2|+|y1﹣y2|叫做P1、P2两点间的直角距离,记作d(P1,P2).
(1)令P0(2,﹣3),O为坐标原点,则d(O,P0)= ;
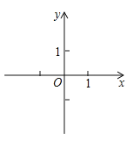
(2)已知O为坐标原点,动点P(x,y)满足d(O,P)=1,请写出x与y之间满足的关系式,并在所给的直角坐标系中画出所有符合条件的点P所组成的图形;
(3)设P0(x0,y0)是一定点,Q(x,y)是直线y=ax+b上的动点,我们把d(P0,Q)的最小值叫做P0到直线y=ax+b的直角距离. 若P(a,﹣3)到直线y=x+1的直角距离为6,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(-3,y1),B(-1,y2),C(2,y3)在抛物线y= x2上,则y1,y2,y3的大小关系系是__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件是必然事件的是( )
A. 某运动员射击一次击中靶心
B. 抛一枚硬币,正面朝上
C. 3个人分成两组,一定有2个人分在一组
D. 明天一定是晴天
查看答案和解析>>
科目:初中数学 来源: 题型:
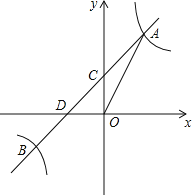
【题目】如图,反比例函数![]() 的图象与一次函数y=kx+b的图象交于点A、B,点A、B的横坐标分别为1,﹣2,一次函数图象与y轴的交于点C,与x轴交于点D.
的图象与一次函数y=kx+b的图象交于点A、B,点A、B的横坐标分别为1,﹣2,一次函数图象与y轴的交于点C,与x轴交于点D.
(1)求一次函数的解析式;
(2)在第三象限的反比例图象上是否存在一个点P,使得S△ODP=2S△OCA?若存在,请求出来P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果ax+b=0,其中a、b为有理数,x为无理数,那么a=0且b=0.
运用上述知识,解决下列问题:
(1)如果(a-2)![]() +b+3=0,其中a、b为有理数,那么a= ,b= ;
+b+3=0,其中a、b为有理数,那么a= ,b= ;
(2)如果(2+![]() )a-(1-
)a-(1-![]() )b=5,其中a、b为有理数,求a+2b的值.
)b=5,其中a、b为有理数,求a+2b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com