
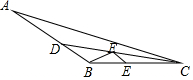
 如图,△ABC中,∠ACB=150°,CD是角平分线,BC=a,AC=b,AB=c,点E、F分别是BC、CD上两点,则BF+EF的最小值是$\frac{ac}{2b}$(用含a、b、c的代数式表示)
如图,△ABC中,∠ACB=150°,CD是角平分线,BC=a,AC=b,AB=c,点E、F分别是BC、CD上两点,则BF+EF的最小值是$\frac{ac}{2b}$(用含a、b、c的代数式表示) 分析 过B作BG⊥AC交CD于F,过F作FE⊥BC于E,于是得到BG的长度等于则BF+EF的最小值,根据相似三角形的判定和性质即可得到结论.
解答  解:过B作BG⊥AC交CD于F,过F作FE⊥BC于E,则BG的长度等于则BF+EF的最小值,
解:过B作BG⊥AC交CD于F,过F作FE⊥BC于E,则BG的长度等于则BF+EF的最小值,
∵BG⊥AC,
作AH⊥CB,
∴∠ABH=30°,
∴AH=$\frac{1}{2}$c,
∵△CBG∽△CAH,
∴$\frac{BG}{\frac{1}{2}c}$=$\frac{a}{b}$,
∴BG=$\frac{ac}{2b}$,
∴BF+EF的最小值是$\frac{ac}{2b}$.
故答案为:$\frac{ac}{2b}$.
点评 本题考查轴对称-最短问题、角平分线性质、相似三角形的判定和性质,解题的关键是找到点E,F的位置,灵活应用垂线段最短解决问题,属于中考常考题型.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 2011年 | 2012年 | 2013年 | 2014年 | |
| 0-14岁人口占总人口的百分比 | 16.4% | 16.5% | 16.4% | 16.5% |
| 15-64岁人口占总人口的百分比 | 74.5% | 74.1% | 73.9% | 73.5% |
| 65岁及以上人口占总人口的百分比 | m | 9.4% | 9.7% | 10.0% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 观察下面由分子是1的分数组成的排列,然后回答问题.
观察下面由分子是1的分数组成的排列,然后回答问题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com