
【题目】△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.

(1)观察猜想
如图1,当点D在线段BC上时,
① BC与CF的位置关系为 ;
② BC,CD,CF之间的数量关系为 .(直接写出结论)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=![]() , CD=
, CD=![]() BC,则GE的长为 .(请直接写出结果)
BC,则GE的长为 .(请直接写出结果)
【答案】(1)①BC⊥CF;②BC=CF+CD;(2)CF⊥BC成立;BC=CD+CF不成立,CD=CF+BC,详见解析;(3)![]() .
.
【解析】
(1) 根据正方形的性质得到∠DAF=∠BAC=90°, 推出△DAB≌△FAC,根据全等三角形的性质即可得到结论;根据全等三角形的性质得到CF=BD, ∠ACF=∠ABD,根据余角的性质即可得到结论;
(2)根据正方形的性质得到∠BAC=∠DAF=90",推出△DAB≌△FAC,根据全等三角形的性质以及等腰三角形的角的性质可得到结论;
(3) 过A作AH⊥BC于H,过E作EM⊥BD于M,EN⊥CF于N,如图3所示,由△ADH≌△DEM,推出EM=DH=3,DM=AH=2, 推出CN=EM=3,EN=CM=3,由△BCG是等腰直角三角形,推出CG=BC=4,推出GN=CG-CN=1,再由勾股定理即可解决问题.
(1)①∵四边形ADEF是正方形,
∴AD=AF,∠DAF=∠BAC=90°,
∴∠BAD=∠CAF,
∵AB=AC,
∴△DAB≌△FAC,
∴∠B=∠ACF,
∴∠ACB+∠ACF=∠ACB+∠ABC=90°,
∴BC⊥CF,
故答案为:BC⊥CF;
②∵△DAB≌△FAC,
∴CF=BD,
∵BC=BD+CD,
∴BC=CF+CD,
故答案为:BC=CF+CD;
(2)CF⊥BC成立;BC=CD+CF不成立,CD=CF+BC,理由如下:
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=∠BAC=90°,
∴∠BAD=∠CAF,
∵AB=AC,
∴△DAB≌△FAC,
∴∠ABD=∠ACF,
∵∠BAC=90°,AB=AC,
∴∠ACB=∠ABC=45°,
∴∠ABD=180°-45°=135°,
∴∠BCF=∠ACF-∠ACB=135°-45°=90°,
∴CF⊥BC,
∵CD=DB+BC,DB=CF,
∴CD=CF+BC;
(3)过A作AH⊥ BC于H,过E作EM⊥BD于M,EN⊥CF于N,如图3所示:
∵∠BAC=90°,AC=AB=![]() ,
,
∴BC=4,
∴CD=![]() BC=1,
BC=1,
∵AH⊥BC,
∴AH=![]() BC=BH=CH=2,
BC=BH=CH=2,
∴DH=CH+CD=3,
∵四边形ADEF是正方形,
∴AD=DE,∠ADE=90°,
∵BC⊥CF,EM⊥BD,EN⊥CF,
∴四边形CMEN是矩形,
∴NE=CM,EM=CN,
∵∠AHD=∠ADE=∠EMD=90°,
∴∠ADH+∠EDM=∠EDM+∠DEM=90",
∴∠ ADH=∠DEM,
∴△ADH≌△DEM (AAS) ,
∴EM=DH=3,DM=AH=2,
∴CN=EM=3, EN=CM=3,
∵∠ABC=45°,
∴∠BGC=45° ,
∴△BCG是等腰直角三角形,
∴CG=BC=4,
∴GN=1,
在Rt△EGN中,EG=![]() .
.
故答案为:![]() .
.



科目:初中数学 来源: 题型:
【题目】已知动点P以每秒1cm的速度沿图甲的边框按从BCDEFA的路径移动,相应的△ABP的面积S与时间t之间的关系如图乙中的图象表示.若AB=3cm,试回答下列问题

(1)图甲中的BC长是多少?
(2)图乙中的a是多少?
(3)图甲中的图形面积是多少?
(4)图乙中的b是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学举行电脑知识竞赛,将八年级两个班参赛学生的成绩(得分均为整数)进行整理后,分成5组,绘制出如下的频数分布直方图(如图),已知图中从左到右的第一、第三、第四、第五小组的频率分别为0.30、0.15、0.10、0.05,第二组的频数是40
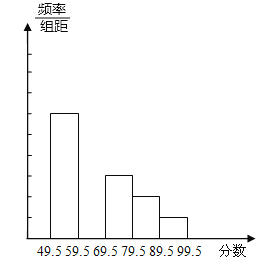
(1)求第二组的频率,并补全这个频数分布直方图;
(2)这两个班参赛的学生人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校课外兴趣小组在本校学生中开展“感动中国2014年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:
类别 | A | B | C | D |
频数 | 30 | 40 | 24 | b |
频率 | a | 0.4 | 0.24 | 0.06 |

(1)表中的a=________,b=________;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为C的人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2013的坐标为

A. (2,1006)B. (1008,0)C. ( -1006,0)D. (1,-1007)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( ).

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=-x+(k+13)和反比例函数![]() 的图象相交于点A与点B.过A点作AC⊥x轴于点C,S△AOC=6.
的图象相交于点A与点B.过A点作AC⊥x轴于点C,S△AOC=6.

(1)求反比例函数和一次函数的解析式;
(2)求点A与点B的坐标;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文化商店计划同时购进A、B两种仪器,若购进A种仪器2台和B种仪器3台,共需要资金1700元;若购进A种仪器3台,B种仪器1台,共需要资金1500元.
(1)求A、B两种型号的仪器每台进价各是多少元?
(2)已知A种仪器的售价为760元/台,B种仪器的售价为540元/台.该经销商决定在成本不超过30000元的前提下购进A、B两种仪器,若B种仪器是A种仪器的3倍还多10台,那么要使总利润不少于21600元,该经销商有哪几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,老师提出利用尺规作图完成下面问题:

已知:∠ACB是△ABC的一个内角.
求作:∠APB=∠ACB.
小路的作法如下:

老师说:“小路的作法正确.”
请回答:(1)点O为△ABC外接圆圆心(即OA=OB=OC)的依据是_____;
(2)∠APB=∠ACB的依据是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com