Question

6．等腰△ABC中，AC=BC，D为BC外一点，连BD、CD，设∠ACB=∠ADB=α．
（1）如图（a），当α=60°时，写出AD，BD，CD三线段之间的数量关系．
（1）如图（b），当α=90°时，写出AD，BD，CD三线段之间的数量关系．
（1）如图（c），当α=120°时，写出AD，BD，CD三线段之间的数量关系．

Answer 1

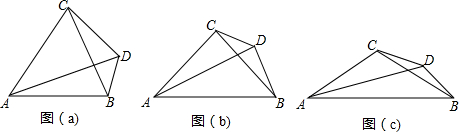
分析 （1）在AD上取一点M使得CM=CD，先证明△MCD是等边三角形，再证明△ACM≌△BCD即可．
（2）在AD上取一点M使得CM=CD，先证明△MCD是等腰直角三角形，再证明再证明△ACM≌△BCD即可．
（3）在AD上取一点M使得CM=CD，先证明MD=$\sqrt{3}$CD，再证明△ACM≌△BCD即可．

解答 解：（1）结论AD=BD+CD．理由如下：
在图（a）中，在AD上取一点M使得CM=CD，
∵CA=CB，∠ACB=60°，
∴△ABC是等边三角形，
∴AC=CB=AB，∠ABC=60°，
∵∠ACB=∠ADB，
∴A、B、D、C四点共圆，
∴∠CDA=∠ABC=60°，
∵CM=CD，
∴△CMD是等边三角形，
∴CM=CD=MD，
∵∠ACB=∠MCD=60°，
∴∠ACM=∠BCD，
在△ACM和△BCD中，
$\left\{\begin{array}{l}{CM=CD}\\{∠ACM=∠BCD}\\{CA=CB}\end{array}\right.$，
∴△ACM≌△BCD，
∴AM=BD，
∴AD=AM+DM=BD+CD．
（2）结论AD-BD=$\sqrt{2}$CD．理由如下：
在图（b）中，在AD上取一点M使得CM=CD，
∵CA=CB，∠ACB=90°，
∴△ABC是等腰直角三角形，
∴∠ABC=45°，
∵∠ACB=∠ADB，
∴A、B、D、C四点共圆，
∴∠CDA=∠ABC=45°，
∵CM=CD，
∴△CMD是等腰直角三角形，
∴∠MCD=90°，DM=$\sqrt{2}$CD，
∵∠ACB=∠MCD=90°，
∴∠ACM=∠BCD，
在△ACM和△BCD中，
$\left\{\begin{array}{l}{CM=CD}\\{∠ACM=∠BCD}\\{CA=CB}\end{array}\right.$，
∴△ACM≌△BCD，
∴AM=BD，
∴AD=AM+DM=BD+$\sqrt{2}$CD，
∴AD-BD=$\sqrt{2}$CD．
（3）结论AD-BD=$\sqrt{3}$CD．理由如下：
如图（c），在AD上取一点M使得CM=CD，
∵CA=CB，∠ACB=120°，
∴∠ABC=30°
∵∠ACB=∠ADB，
∴A、B、D、C四点共圆，
∴∠CDA=∠ABC=30°，
∵CM=CD，
∴∠CMD=∠CDM=30°，∠MCD=120°，易知DM=$\sqrt{3}$CD，
∵∠ACB=∠MCD=120°，
∴∠ACM=∠BCD，
在△ACM和△BCD中，
$\left\{\begin{array}{l}{CM=CD}\\{∠ACM=∠BCD}\\{CA=CB}\end{array}\right.$，
∴△ACM≌△BCD，
∴AM=BD，
∴AD=AM+MD=BD+$\sqrt{3}$CD，
∴AD-BD=$\sqrt{3}$CD．

点评 本题考查全等三角形的判定和性质、等边三角形的判定和性质、等腰直角三角形的判定和性质，探究形变后结论发生什么变化，通过构造特殊三角形，利用三角形全等解决问题．