
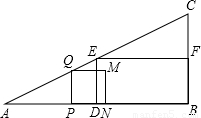
 ,即0<x≤
,即0<x≤ 时,此时正方形与矩形没有重合,因此y=0;
时,此时正方形与矩形没有重合,因此y=0; <x≤4,此时正方形与矩形重合的面积应该是以DN为长,NM为宽的矩形,DN=PN-PD=PN-(AD-AP)=x-(4-
<x≤4,此时正方形与矩形重合的面积应该是以DN为长,NM为宽的矩形,DN=PN-PD=PN-(AD-AP)=x-(4- x)=
x)= x-4.而NM=PQ=
x-4.而NM=PQ= x,因此重合部分的面积应该是y=(
x,因此重合部分的面积应该是y=( x-4)×
x-4)× x=
x= x2-2x;
x2-2x;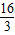 时,此时正方形重合部分的面积应该是以正方形边长为长,DE为宽的矩形的面积,PN=
时,此时正方形重合部分的面积应该是以正方形边长为长,DE为宽的矩形的面积,PN= x,DE=2,因此此时重合部分的面积是y=
x,DE=2,因此此时重合部分的面积是y= x×2=x;
x×2=x;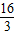 <x<8时,此时重合部分的面积应该是以DE长为宽,PA长为长的矩形的面积.BP=AB-AP=8-x,BF=DE=2,因此此时重合部分的面积应该是y=(8-x)×2=16-2x.
<x<8时,此时重合部分的面积应该是以DE长为宽,PA长为长的矩形的面积.BP=AB-AP=8-x,BF=DE=2,因此此时重合部分的面积应该是y=(8-x)×2=16-2x. =1.5cm,
=1.5cm, ,y=0;
,y=0; <x≤4,y=
<x≤4,y=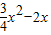 ,
,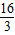 ,y=x;
,y=x;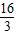 <x<8,y=16-2x;
<x<8,y=16-2x;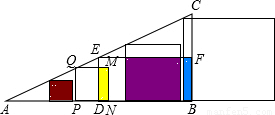
 <x≤4时,如果y=2,2=
<x≤4时,如果y=2,2=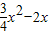 ,解得x=
,解得x=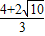 或x=
或x=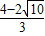 (舍去);
(舍去);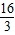 时,如果y=2,x=2,也不符合题意,
时,如果y=2,x=2,也不符合题意,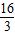 <x<8时,如果y=2,2=16-2x,解得x=7,因此当AP=7cm时,y=2cm2.
<x<8时,如果y=2,2=16-2x,解得x=7,因此当AP=7cm时,y=2cm2.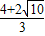 cm时,y=2cm2.
cm时,y=2cm2.

科目:初中数学 来源:2001年全国中考数学试题汇编《四边形》(02)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2001年全国中考数学试题汇编《反比例函数》(01)(解析版) 题型:解答题
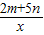 的图象都过点(1,-2),求:
的图象都过点(1,-2),求:查看答案和解析>>
科目:初中数学 来源:2001年天津市中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2001年天津市中考数学试卷(解析版) 题型:解答题
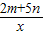 的图象都过点(1,-2),求:
的图象都过点(1,-2),求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com