
| A. | 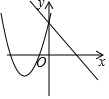 | B. | 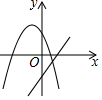 | C. | 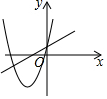 | D. | 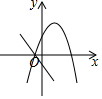 |
分析 可先由一次函数y=ax+b图象得到字母系数的正负,再与二次函数y=ax2+bx+c的图象相比较看是否一致.
解答 解:A、由抛物线可知,a>0,由直线可知,a<0,故本选项错误;
B、由抛物线可知,a<0,x=-$\frac{b}{2a}$>0,得b>0,由直线可知,a>0,b>0,故本选项错误;
C、由抛物线可知,a>0,x=-$\frac{b}{2a}$<0,得b>0,由直线可知,a>0,b<0,故本选项错误;
D、由抛物线可知,a<0,x=-$\frac{b}{2a}$>0,得b>0,由直线可知,a<0,b>0,故本选项正确.
故选:D.
点评 本题考查抛物线和直线的性质,用假设法来搞定这种数形结合题是一种很好的方法.


科目:初中数学 来源: 题型:解答题
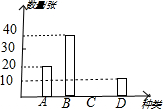 假期,某学校组织学生分别到A、B,C、D四个地方进行研习旅行,学校按定额购买了前往四地的车票,如图是未制作完成的车票种类和数量的条形统计图,请根据统计图回答下列问题:
假期,某学校组织学生分别到A、B,C、D四个地方进行研习旅行,学校按定额购买了前往四地的车票,如图是未制作完成的车票种类和数量的条形统计图,请根据统计图回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
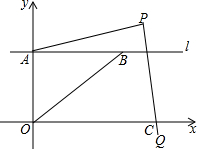 如图,在平面直角坐标系中,直线l∥x轴,交y轴于点A,第一象限内的点B在直线l上,连接OB,动点P满足∠APQ=90°,PQ交x轴于点C,
如图,在平面直角坐标系中,直线l∥x轴,交y轴于点A,第一象限内的点B在直线l上,连接OB,动点P满足∠APQ=90°,PQ交x轴于点C,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
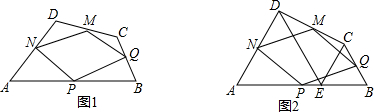
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
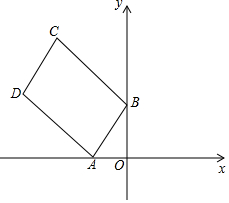 如图,在直角坐标系中,点A,B分别在x轴负半轴、y轴正半轴上,
如图,在直角坐标系中,点A,B分别在x轴负半轴、y轴正半轴上,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点P将线段AB分割成两条线段AP、PB,且AP:AB=PB:AP,那么点P就叫做线段AB的黄金分割点;若AB=3,那么AP的长为$\frac{-3+3\sqrt{3}}{2}$.
如图,点P将线段AB分割成两条线段AP、PB,且AP:AB=PB:AP,那么点P就叫做线段AB的黄金分割点;若AB=3,那么AP的长为$\frac{-3+3\sqrt{3}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com