
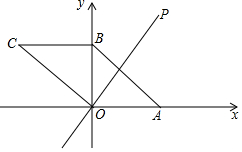
 如图,在平面直角坐标系xOy中,?ABCO的顶点A,B的坐标分别是A(3,0),B(0,2).动点P在直线y=$\frac{3}{2}$x上运动,以点P为圆心,PB长为半径的⊙P随点P运动,当⊙P与?ABCO的边相切时,P点的坐标为(0,0)或($\frac{2}{3}$,1)或(3-$\sqrt{5}$,$\frac{9-3\sqrt{5}}{2}$).
如图,在平面直角坐标系xOy中,?ABCO的顶点A,B的坐标分别是A(3,0),B(0,2).动点P在直线y=$\frac{3}{2}$x上运动,以点P为圆心,PB长为半径的⊙P随点P运动,当⊙P与?ABCO的边相切时,P点的坐标为(0,0)或($\frac{2}{3}$,1)或(3-$\sqrt{5}$,$\frac{9-3\sqrt{5}}{2}$). 分析 设P(x,$\frac{3}{2}$x),⊙P的半径为r,由题意BC⊥y轴,直线OP的解析式y=$\frac{3}{2}$x,直线OC的解析式为y=-$\frac{2}{3}$x,可知OP⊥OC,分分四种情形讨论即可.
解答 解:①当⊙P与BC相切时,∵动点P在直线y=$\frac{3}{2}$x上,
∴P与O重合,此时圆心P到BC的距离为OB,
∴P(0,0).
②如图1中,当⊙P与OC相切时,则OP=BP,△OPB是等腰三角形,作PE⊥y轴于E,则EB=EO,易知P的纵坐标为1,可得P($\frac{2}{3}$,1).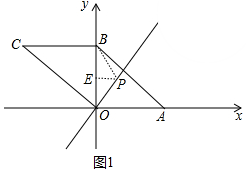
③如图2中,当⊙P与OA相切时,则点P到点B的距离与点P到x轴的距离相等,可得$\sqrt{{x}^{2}+(\frac{3}{2}x-2)^{2}}$=$\frac{3}{2}$x,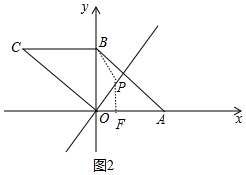
解得x=3+$\sqrt{5}$或3-$\sqrt{5}$,
∵x=3+$\sqrt{5}$>OA,
∴⊙P不会与OA相切,
∴x=3+$\sqrt{5}$不合题意,
∴P(3-$\sqrt{5}$,$\frac{9-3\sqrt{5}}{2}$).
④如图3中,当⊙P与AB相切时,设线段AB与直线OP的交点为G,此时PB=PG,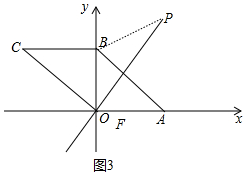
∵OP⊥AB,
∴∠BGP=∠PBG=90°不成立,
∴此种情形,不存在P.
综上所述,满足条件的P的坐标为(0,0)或($\frac{2}{3}$,1)或(3-$\sqrt{5}$,$\frac{9-3\sqrt{5}}{2}$).
点评 本题考查切线的性质、一次函数的应用、勾股定理、等腰三角形的性质等知识,解题的关键是学会利用参数解决问题,学会用分类讨论的思想思考问题,属于中考填空题中的压轴题.


科目:初中数学 来源: 题型:解答题
| 型号 金额 | Ⅰ型设备 | Ⅱ型设备 | |||
| 购买金额x(万元) | x | 1 | x | 2 | 4 |
| 补贴金额y(万元) | y1=kx(k≠0) | 0.4 | y2=ax2+bx(a≠0) | 2.4 | 3.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AD=BC,∠B=∠D,AD不平行于BC,过点C作CE∥AD交△ABC的外接圆O于点E,连接AE.
如图,在四边形ABCD中,AD=BC,∠B=∠D,AD不平行于BC,过点C作CE∥AD交△ABC的外接圆O于点E,连接AE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售价格x(元/千克) | 30 | 35 | 40 | 45 | 50 |
| 日销售量p(千克) | 600 | 450 | 300 | 150 | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
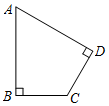 已知:如图,四边形ABCD中,∠ABC=∠ADC=90°,AB=AD.
已知:如图,四边形ABCD中,∠ABC=∠ADC=90°,AB=AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
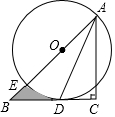 如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.
如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com