
分析 根据比例线段的概念:如果其中两条线段的乘积等于另外两条线段的乘积,则四条线段叫成比例线段.
解答 解:根据比例线段的概念:要求第四个数,只需让其中的任何两个数相乘,再除以第三个数,即可求得第四个数.
即是$\sqrt{3}$×2÷$\sqrt{6}$=$\sqrt{2}$,或$\sqrt{3}$×$\sqrt{6}$÷2=$\frac{3\sqrt{2}}{2}$,或2×$\sqrt{6}$÷$\sqrt{3}$=2$\sqrt{2}$.
故所求的线段的长度为$\sqrt{2}$或$\frac{3\sqrt{2}}{2}$或2$\sqrt{2}$.
点评 本题考查了比例线段的概念,正确求解第四个数:让其中的任何两个数相乘,再除以第三个数.


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
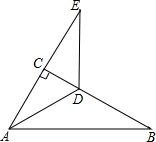 如图,△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB,延长AC至E,使CE=AC.
如图,△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB,延长AC至E,使CE=AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com