
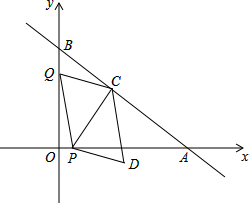
 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��AB��x�ᣬy��ֱ��ڵ�A��8��0����B��0��6��������P�ӵ�O��������x����������ÿ��1����λ���ٶ��˶���ͬʱ����Q�ӵ�B������������BO������ÿ��2����λ���ٶ��˶�������P��PC��AB�ڵ�C������PQ��CQ����PQ��CQΪ�ڱ߹���?PQCD�����P�˶���ʱ��Ϊt�룮
��ͼ����ƽ��ֱ������ϵ�У�ֱ��AB��x�ᣬy��ֱ��ڵ�A��8��0����B��0��6��������P�ӵ�O��������x����������ÿ��1����λ���ٶ��˶���ͬʱ����Q�ӵ�B������������BO������ÿ��2����λ���ٶ��˶�������P��PC��AB�ڵ�C������PQ��CQ����PQ��CQΪ�ڱ߹���?PQCD�����P�˶���ʱ��Ϊt�룮���� ��1���������AB����RT��ACP�У�PA=8-t������sin��OAB=$\frac{PC}{PA}$=$\frac{OB}{AB}$�����PC������cos��OAB=$\frac{OA}{AB}$=$\frac{AC}{PA}$�����AC��
��2�����ٵ�D��x����ʱ����ͼ2�У���QC��OA����$\frac{BQ}{BO}$=$\frac{BC}{AB}$���ɴ˼��ɽ�����⣮
�ڵ���D��AB��ʱ����ͼ3�У���PQ��AB����$\frac{OQ}{OB}$=$\frac{OP}{OA}$�����ʱ��t������٢���������ʱ�ġ�POQ��������ɽ�����⣮
��3����ͼ4�У���QC���M����ʱ����QC��CM������֤��QB=QC����QN��BC��N������cos��ABO=$\frac{BO}{AB}$=$\frac{BN}{BQ}$���г����̼��ɽ�����⣬��CQ���ǡ�M����ʱ���������ƣ�
��� �⣺��1����ͼ1�У�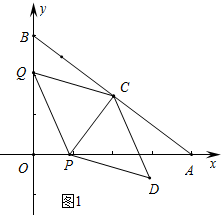
��OA=8��OB=6��
��AB=$\sqrt{O{B}^{2}+O{A}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10��
��RT��ACP��PA=8-t��
��sin��OAB=$\frac{PC}{PA}$=$\frac{OB}{AB}$��
��PC=$\frac{3}{5}$��8-t����
��cos��OAB=$\frac{OA}{AB}$=$\frac{AC}{PA}$��
��AC=$\frac{4}{5}$��8-t����
��2���ٵ�D��x����ʱ����ͼ2�У�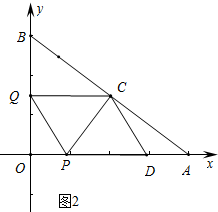
��QC��OA��
��$\frac{BQ}{BO}$=$\frac{BC}{AB}$��
��$\frac{2t}{6}$=$\frac{10-\frac{4}{5}��8-t��}{10}$��
���t=$\frac{27}{19}$��
��t=$\frac{27}{19}$ʱ����D��x���ϣ�
�ڵ���D��AB��ʱ����ͼ3�У�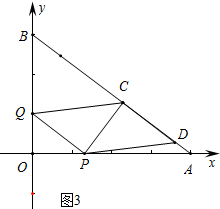
��PQ��AB��
��$\frac{OQ}{OB}$=$\frac{OP}{OA}$��
��$\frac{6-2t}{6}$=$\frac{t}{8}$��
��t=$\frac{24}{11}$��
��t=$\frac{27}{19}$ʱ��S=$\frac{1}{2}$•��6-2t��•t=$\frac{810}{361}$��
��t=$\frac{24}{11}$ʱ��S=$\frac{1}{2}$•��6-2t��•t=$\frac{216}{121}$��
���D���ڡ�ABO�ڲ����������߽磩ʱ��ֱ��д��S��ȡֵ��Χ
$\frac{216}{121}$��S��$\frac{810}{361}$��
��3����ͼ4�У�
��Q��0��6-2t����Q�䣨0��2t-6����M��$\frac{8+t}{2}$��0����
��QC���M����ʱ����QC��CM��
���QCM=90�㣬
���QCP+��PCM=90�㣬�ߡ�QCP+��QCB=90�㣬
���BCQ=��PCM=��CPM��
�ߡ�CPM+��PAC=90�㣬��OBA+��OAB=90�㣬
���APC=��OBA��
���QBC=��QCB��
��BQ=CQ����QN��BC��N��
��cos��ABO=$\frac{BO}{AB}$=$\frac{BN}{BQ}$��
��$\frac{\frac{1}{2}[10-\frac{4}{5}��8-t��]}{2t}$=$\frac{6}{10}$��
���t=$\frac{9}{4}$��
��CQ���ǡ�M����ʱ��ͬ���ɵ�$\frac{\frac{1}{2}[10-\frac{4}{5}��8-t��]}{12-2t}$=$\frac{6}{10}$�����t=$\frac{27}{8}$��
��t=$\frac{9}{4}$��$\frac{27}{8}$ʱ����A��P��C�����Բ���CQQ�������е�һ�������У�
���� ���⿼��Բ���ۺ��⡢������Ǻ�����ƽ���ı��ε����ʡ����������ε����ʡ����ߵ����ʵ�֪ʶ������Ĺؼ�����õ�D������λ��ʱ��ʱ�䣬ѧ�����÷��̽�����⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��3 | B�� | x��3��x��-3 | C�� | x��0��x��-3 | D�� | x��-3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
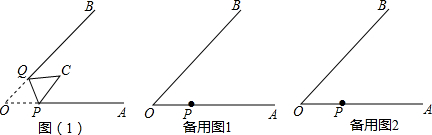
 ��ͼ�����κ���$y=\frac{1}{2}{��x-3��^2}-1$��ͼ����x�ύ��A��B���㣨��A�ڵ�B��ࣩ����y�ύ�ڵ�C������ΪD��
��ͼ�����κ���$y=\frac{1}{2}{��x-3��^2}-1$��ͼ����x�ύ��A��B���㣨��A�ڵ�B��ࣩ����y�ύ�ڵ�C������ΪD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
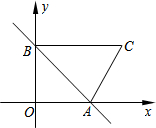 ��֪һ�κ���y=-x+3��ͼ����x�ύ�ڵ�A����y�ύ�ڵ�B��BC��x�ᣬ�ҡ�ACB������ֵΪ3��
��֪һ�κ���y=-x+3��ͼ����x�ύ�ڵ�A����y�ύ�ڵ�B��BC��x�ᣬ�ҡ�ACB������ֵΪ3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
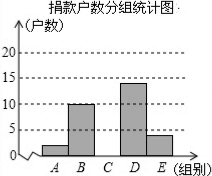 Ϊ���ø����ʧѧ��ͯ�ط�У��ij������֯���װ��������֡���������������־������е���ͷ���ͳ�ƺ�������������ͼ��ʾ��ͳ��ͼ��ͼ����Ϣ����������
Ϊ���ø����ʧѧ��ͯ�ط�У��ij������֯���װ��������֡���������������־������е���ͷ���ͳ�ƺ�������������ͼ��ʾ��ͳ��ͼ��ͼ����Ϣ����������| ��� | ���x��Ԫ | ���� | Ƶ�� |
| A | 1��x��100 | 2 | 0.04 |
| B | 100��x��200 | 10 | 0.2 |
| C | 200��x��300 | 0.4 | |
| D | 300��x��400 | 14 | a |
| E | x��400 | 4 | 0.08 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com