
如图, 在Rt△ABC中,∠C=90º, AC=9,BC=12,动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ. 点P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).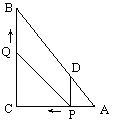
(1)直接用含t的代数式分别表示:QB=__________, PD=___________;
(2)是否存在t的值,使四边形PDBQ为平行四边形?若存在,求出t的值;若不存在,说明理由;
(3)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变点Q的速度(匀速运动),使四边形PDBQ在某一时刻成为菱形,求点Q的速度.
(1)QB=12-2t,PD=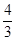 t (2)t=
t (2)t=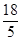 秒,或t=3.6秒。(3)t=5秒,Q的速度为
秒,或t=3.6秒。(3)t=5秒,Q的速度为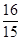 。
。
解析试题分析:解:(1)QB=12-2t, PD=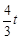 .
.
(2)∵PD∥BC,当PD=BQ时四边形PDBQ为平行四边形,
即12-2t=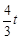 ,解得:
,解得: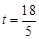 (秒) (或
(秒) (或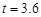 秒)
秒)
∴存在t的值,使四边形PDBQ为平行四边形.
(3)∵t=3.6时,BQ=PD=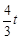 =4.8,由△ABC∽△ADP,∴AD=
=4.8,由△ABC∽△ADP,∴AD=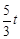 =6, BD=15-6=9,
=6, BD=15-6=9,
∴BD≠PD,∴不存在t使四边形PDBQ为菱形.
设Q以每秒a个单位长度的速度运动,则PD=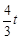 , BD=15-
, BD=15-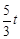 ,QB=12-at,
,QB=12-at,
四边形PDBQ为菱形时,有PD=BD=BQ,先由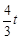 =15-
=15-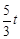 得t=5
得t=5
将t=5代入12-at=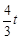 ,解得
,解得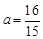
考点:平行四边判定,菱形判定,相似三角形性质,直角三角形性质。
点评:熟知以上判定条件性质,在解答题目时要认真审题,有三问需结合已知一一作答,注意的是,二问有两种情况,易遗漏,本题有一定的难度属于中档题。


科目:初中数学 来源: 题型:
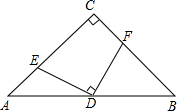 已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC,D是AB的中点,E、F分别在AC、BC上,且ED⊥FD.求证:S四边形EDFC=
已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC,D是AB的中点,E、F分别在AC、BC上,且ED⊥FD.求证:S四边形EDFC=| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•湛江模拟)如图,在Rt△AB′C′中,∠AC′B′=90°,∠B′AC′=45°,B′C′=3,Rt△ABC可以看作是由Rt△AB′C′绕点A顺时针方向旋转45°得到的,则AC的长为
(2012•湛江模拟)如图,在Rt△AB′C′中,∠AC′B′=90°,∠B′AC′=45°,B′C′=3,Rt△ABC可以看作是由Rt△AB′C′绕点A顺时针方向旋转45°得到的,则AC的长为查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△AB′C′中,∠AC′B′=90°,∠B′AC′=45°,B′C′=3,Rt△ABC可以看作是由Rt△AB′C′绕点A顺时针方向旋转45°得到的,则AC的长为________.
如图,在Rt△AB′C′中,∠AC′B′=90°,∠B′AC′=45°,B′C′=3,Rt△ABC可以看作是由Rt△AB′C′绕点A顺时针方向旋转45°得到的,则AC的长为________.查看答案和解析>>
科目:初中数学 来源:2012年广东省湛江市中考调研数学试卷(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com