
【题目】如图,在平面直角坐标系中,直线 ![]() 分别与x轴、y轴交于点B、C,且与直线
分别与x轴、y轴交于点B、C,且与直线 ![]() 交于点A.
交于点A.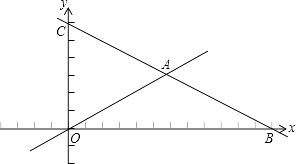
(1)分别求出点A、B、C的坐标;
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的函数表达式;
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
【答案】
(1)解:直线 ![]() ,
,
当x=0时,y=6,
当y=0时,x=12,
∴B(12,0),C(0,6),
解方程组: 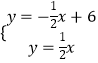 得:
得: ![]() ,
,
∴A(6,3),
答:A(6,3),B(12,0),C(0,6).
(2)解:设D(x, ![]() x),
x),
∵△COD的面积为12,
∴ ![]() ×6×x=12,
×6×x=12,
解得:x=4,
∴D(4,2),
设直线CD的函数表达式是y=kx+b,把C(0,6),D(4,2)代入得:
![]() ,
,
解得: ![]() ,
,
∴y=﹣x+6,
答:直线CD的函数表达式是y=﹣x+6.
(3)解:答:存在点Q,如图,
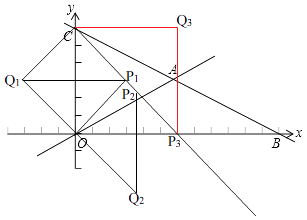
使以O、C、P、Q为顶点的四边形是菱形,点Q的坐标是(6,6)或(﹣3,3)或 ![]() .
.
【解析】(1)由两函数解析式联立方程,可求出点A的坐标,由直线直线 l 1 的解析式,根据x=0和y=0,建立方程即可求出点B、C的坐标。
(2)已知D是线段OA上的点,可知点D在第一象限,设点D的坐标,根据△COD的面积公式即可求出点D的坐标,再用待定系数法求出直线CD的函数解析式。
(3)要求以O、C、P、Q为顶点的四边形是菱形时,点Q的坐标,分情况讨论,当以OC=6为边时,有两种情况(点Q在第一象限和第四象限);当以OC为对角线时,根据题意易求出点Q的坐标。
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法,以及对菱形的性质的理解,了解菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.


科目:初中数学 来源: 题型:
【题目】已知如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.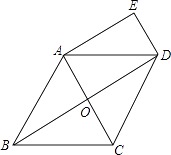
(1)求证:四边形AODE是矩形;
(2)若AB=6,∠BCD=120°,求四边形AODE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如同,△ABC内接于⊙O,且半径OC⊥AB,点D在半径OB的延长线上,且∠A=∠BCD=30°,AC=2,则由 ![]() ,线段CD和线段BD所围成图形的阴影部分的面积为 .
,线段CD和线段BD所围成图形的阴影部分的面积为 . 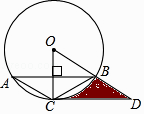
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市美化工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天;若由甲队先做20天,剩下的工程由甲、乙合做24天可完成.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲乙两队全程合作完成该工程省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【新知理解】
如图①,点C在线段AB上,图中共有三条线段AB、AC和BC,若其中有一条线段的长度是另外一条线段长度的2倍,则称点C是线段AB的“巧点”.
线段的中点__________这条线段的“巧点”;(填“是”或“不是”).
若AB = 12cm,点C是线段AB的巧点,则AC=___________cm;
【解决问题】
(3) 如图②,已知AB=12cm.动点P从点A出发,以2cm/s的速度沿AB向点B匀速移动:点Q从点B出发,以1cm/s的速度沿BA向点A匀速移动,点P、Q同时出发,当其中一点到达终点时,运动停止,设移动的时间为t(s).当t为何值时,A、P、Q三点中其中一点恰好是另外两点为端点的线段的巧点?说明理由

![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(知识情境)通常情况下,用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.
(1)如图1,在边长为![]() 的正方形中挖掉一个边长为
的正方形中挖掉一个边长为![]() 的小正方形
的小正方形![]() .把余下的部分剪拼成一个长方形(如图2).通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是______________;
.把余下的部分剪拼成一个长方形(如图2).通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是______________;
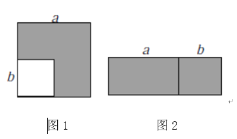
(拓展探究)类似地,用两种不同的方法计算同一个几何体的体积,也可以得到一个恒等式.
如图3是边长为![]() 的正方体,被如图所示的分割线分成
的正方体,被如图所示的分割线分成![]() 块.
块.
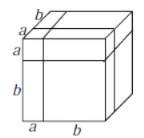
图3
(2)用不同的方法计算这个正方体的体积,就可以得到一个恒等式,这个恒等式可以为:
_________________________________________________________________;
(3)已知![]() ,
,![]() ,利用上面的恒等式求
,利用上面的恒等式求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OD平分∠BOF,OE⊥CD于O,若∠EOF=α,下列说法①∠AOC=α﹣90°;②∠EOB=180°﹣α;③∠AOF=360°﹣2α,其中正确的是( )
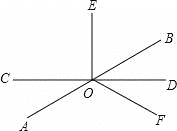
A. ①②B. ①③C. ②③D. ①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com