
 已知:如图,∠BAC=30°,G为∠BAC平分线上一点,EG∥AC,EG交AB于点E;GD⊥AC,垂足为点D.求证:GD=$\frac{1}{2}$EG.
已知:如图,∠BAC=30°,G为∠BAC平分线上一点,EG∥AC,EG交AB于点E;GD⊥AC,垂足为点D.求证:GD=$\frac{1}{2}$EG. 分析 作辅助线GF⊥AB,根据角平分线的性质可知GF=GD,由EG∥AC可知∠2=∠EGA,从而推出∠3与∠BAC的关系,从而得出GE与GF的关系,进而得到GE与GD的关系.
解答 证明:如下图所示:作GF⊥AB于点F,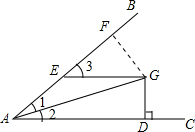
∵AG为∠BAC平分线,GF⊥AB,GD⊥AC,
∴∠1=∠2,GF=GD.
∵EG∥AC,
∴∠2=∠EGA.
∴∠1+∠EGA=∠1+∠2=∠BAC.
∵∠BAC=30°,∠3=∠1+∠EGA,
∴∠3=30°.
∵GF⊥AB,
∴GE=2GF.
又∵GF=GD,
∴GE=2GD.
即$GD=\frac{1}{2}GE$.
点评 本题考查角平分线的性质角、平行线的性质和在直角三角形中30°角所对的直角边与斜边的关系,关键是正确分析题目,灵活变化最终求得结论成立.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:填空题
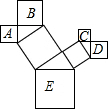 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、4、2、3,则最大正方形E的面积是38.
如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、4、2、3,则最大正方形E的面积是38.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
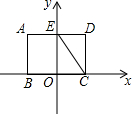 以矩形ABCD的边BC的中点O为原点,建立如图所示的平面直角坐标系,边AD交y轴于点E,连接CE.已知OC、OE的长是关于x的一元二次方程x2-5x+6=0的两个根,且OC<OE.
以矩形ABCD的边BC的中点O为原点,建立如图所示的平面直角坐标系,边AD交y轴于点E,连接CE.已知OC、OE的长是关于x的一元二次方程x2-5x+6=0的两个根,且OC<OE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com