
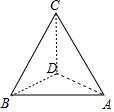
 如图,为了估测某塔的高度,在同一水平面的A,B两点处进行测量.在点A处测得塔顶C在西偏北20°的方向上,仰角为60°;在点B处侧得塔顶C在东偏北40°的方向上,仰角为30°,若A,B两点相距130m,则塔的高度CD=10$\sqrt{39}$m.
如图,为了估测某塔的高度,在同一水平面的A,B两点处进行测量.在点A处测得塔顶C在西偏北20°的方向上,仰角为60°;在点B处侧得塔顶C在东偏北40°的方向上,仰角为30°,若A,B两点相距130m,则塔的高度CD=10$\sqrt{39}$m. 分析 根据方位角求出∠ADB,利用仰角的正切值得出AD,BD关系,在△ABD中使用余弦定理解出AD,BD,从而得出CD.
解答 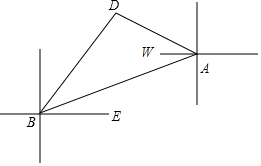 解:作出平面ABD的方位图如图所示:
解:作出平面ABD的方位图如图所示:
由题意可知∠WAD=20°,∠EAD=40°,
设∠ABE=θ,则∠WAB=θ,
∴∠DBA+∠DAB=40°-θ+20°+θ=60°,
∴∠ABD=120°,
设BD=x,AD=y,则由余弦定理得:AB2=x2+y2-2xycos∠ADB,
即16900=x2+y2+xy.
在Rt△BCD中,
∵tan∠CBD=$\frac{CD}{BD}$=$\frac{CD}{x}$=$\frac{\sqrt{3}}{3}$,
∴CD=$\frac{\sqrt{3}x}{3}$,
在Rt△ACD中,∵tan∠CAD=$\frac{CD}{AD}$=$\frac{CD}{y}$,
∴CD=$\sqrt{3}$y,
∴x=3y,
解方程组$\left\{\begin{array}{l}{16900={x}^{2}+{y}^{2}+xy}\\{x=3y}\end{array}\right.$得$\left\{\begin{array}{l}{x=30\sqrt{13}}\\{y=10\sqrt{13}}\end{array}\right.$.
∴CD=$\sqrt{3}$y=10$\sqrt{39}$.
故答案为:10$\sqrt{39}$.
点评 本题考查了解三角形的实际应用,根据题意画出图形,求出∠ADB及AD,BD的关系是解题关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
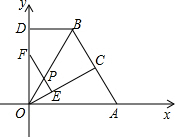 如图,OA=OB=10,AB=12,点A在x轴正半轴上,过点O作OC⊥AB于点C,作BD垂直y轴于D,若动点E从原点O出发,沿线段OC向终点C运动,动点F从点D出发,沿线段DO向终点O运动,两点同时出发,速度均为每秒1个单位长度,设运动的时间为t秒.
如图,OA=OB=10,AB=12,点A在x轴正半轴上,过点O作OC⊥AB于点C,作BD垂直y轴于D,若动点E从原点O出发,沿线段OC向终点C运动,动点F从点D出发,沿线段DO向终点O运动,两点同时出发,速度均为每秒1个单位长度,设运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
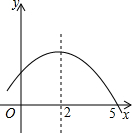 如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c>0的解集是( )
如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c>0的解集是( )| A. | -1<x<5 | B. | x>5 | C. | x<-1 | D. | x<-1或x>5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ② | C. | ③ | D. | ②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 日期 | 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
| 吨数 | +11 | -12 | -16 | +35 | -23 | -20 | -15 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com