练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．计算
    （1）|-3|+（$\frac{1}{3}$）-2×（$π-\sqrt{3}$）0+（-1）2         
    （2）$\frac{{x}^{2}-2x+1}{{x}^{2}-1}$÷$\frac{x-1}{{x}^{2}+x}$．

    分析 （1）根据绝对值、负指数幂、零指数幂进行计算即可；
    （2）先因式分解，再约分即可．

    解答 解：（1）原式=3+9+1
    =13；
    （2）原式=$\frac{（x-1）^{2}}{（x+1）（x-1）}$•$\frac{x（x+1）}{x-1}$
    =x．

    点评 本题考查了分式的乘除法以及零指数幂、负整数指数幂，掌握它们的运算法则是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    7．二次函数y=x2+2x+4的最小值为（　　）
    A．3B．4C．5D．6

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

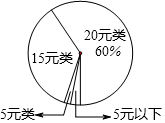    8．某校为了了解2015年九年级学生在某次为贫困山区小朋友的捐款情况，从中随机抽取了40名学生的捐款金额（元）进行统计分析．统计中发现这40名同学的捐款金额可分为20元、15元、5元、5元以下，并按捐款金额分为4类，各类的合计捐款数（元）如下表，各类的合计捐款数（元）如下扇形统计图．其中20元类的合计捐款数占这40名同学的总捐款数的60%．
    类别20元类15元类5元类5元以下
    各类合计捐款数360m510
    （1）求表中字母m的值及扇形统计图中“15元类”所对应的圆心角的度数．
    （2）该校九年级共1200人，请估计捐款金额不低于15元的学生人数．
    （3）据了解，样本中捐款金额为5元以下的同学的捐款金额为2元或1元，若从样本中捐款金额为5元以下的同学中随机抽取1位同学，求所抽同学的捐款金额为2元的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．已知平行四边形ABCD的两邻边AB、AD的长是关于x的一元二次方程x2-mx+$\frac{m}{2}$-$\frac{1}{4}$=0的两个实数根．
    （1）当m为何值时，四边形ABCD是菱形？
    （2）若AB的长为2，那么平行四边形ABCD的周长是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

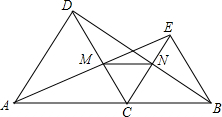    12．如图，点C是线段AB上除点A、B外的任意一点，分别以AC、BC为边在线段AB的同旁作等边△ACD和等边△BCE，连接AE交DC于M，连接BD交CE于N，连接MN．
    （1）求证：AE=BD；
    （2）求证：MN∥AB．
    （3）设AE和DB的交点为F，连FC，求证：FC平分∠AFB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．已知a为正整数，关于x的方程$\frac{3}{2}x-a=\frac{4}{5}$x+41的解为整数，则a的最小值为（　　）
    A．8B．6C．2D．1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．某水果批发商场经销一种高档水果，如果每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，若每千克涨价一元，日销售量将减少20千克．设每千克水果盈利x（x＞10）元，每天销售这种水果的盈利为y元．
    （1）求出y关于x的函数关系式；
    （2）每千克水果盈利多少元时，能使商场每天销售这种水果获利最多，最多获利多少元？
    （3）现要保证每天销售这种水果盈利6000元以上（含6000元），求每千克水果盈利的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．在3×3的正方形格点图中，△ABC和△DEF是关于某条直线成轴对称的两个格点三角形，现给出了△ABC，在下面的图中画出5个符合条件的△DEF，并画出对称轴．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．（1）$\sqrt{12}$+$\sqrt{27}$+$\frac{1}{4}$$\sqrt{48}$-15$\sqrt{\frac{1}{3}}$
    （2）（2$\sqrt{3}$+$\sqrt{5}$）2-（2$\sqrt{3}$-$\sqrt{5}$）2
    （3）$\left\{\begin{array}{l}{2a+3b=2}\\{4a-9b=-1}\end{array}\right.$
    （4）$\left\{\begin{array}{l}{3x+2y=21}\\{2x-y=14}\end{array}\right.$．

    查看答案和解析>>

    同步练习册答案