
 如图,一段抛物线:y=2x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…,如此进行下去,直至的C10,(1)请写出抛物线C2的解析式:y=-2(x-3)(x-6);(2)若P(17,m)在第10段抛物线C10上,则m=-260.
如图,一段抛物线:y=2x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…,如此进行下去,直至的C10,(1)请写出抛物线C2的解析式:y=-2(x-3)(x-6);(2)若P(17,m)在第10段抛物线C10上,则m=-260. 分析 (1)根据图象的旋转变化规律以及二次函数的平移规律得出平移后解析式,
(2)利用已知得出图象与x轴交坐标变化规律,进而求出a的值.
解答 解:(1)∵一段抛物线:y=2x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,
∴C1过(0,0),(3,0)两点,
∴抛物线C2的解析式二次项系数为:-2,且过点(3,0),(6,0),
∴y=-2(x-3)(x-6);
故答案为:y=-2(x-3)(x-6);
(2)∵一段抛物线:y=2x(x-3)(0≤x≤3),
∴图象与x轴交点坐标为:(0,0),(3,0),
∵将C1绕点A1旋转180°得C2,交x轴于点A2;
将C2绕点A2旋转180°得C3,交x轴于点A3;
…
如此进行下去,直至得C10.
∴C10的与x轴的交点横坐标为(27,0),(30,0),且图象在x轴上方,
∴C10的解析式为:y10=-2(x-27)(x-30),
当x=17时,y=-2(17-27)×(17-30)=-260.
故答案为:-260.
点评 此题主要考查了二次函数的平移规律,根据已知得出二次函数旋转后解析式是解题关键.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:选择题
| A. | k=-2,b=-4 | B. | k=2,b=-4 | C. | k=-4,b=2 | D. | k=4,b=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=$\frac{1}{2}$(x-1)2-$\frac{1}{2}$ | B. | y=$\frac{1}{2}$(x-$\frac{1}{4}$)2+$\frac{1}{32}$ | C. | y=$\frac{1}{2}$(x-1)2+$\frac{1}{2}$ | D. | y=$\frac{1}{2}$(x-$\frac{1}{4}$)2-$\frac{1}{32}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
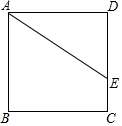 已知正方形ABCD中,点E在边DC上,DE=3,EC=1,如图所示,把线段AE绕点A旋转,使点E落在直线BC上的点F处,则F、C两点的距离为1或7.
已知正方形ABCD中,点E在边DC上,DE=3,EC=1,如图所示,把线段AE绕点A旋转,使点E落在直线BC上的点F处,则F、C两点的距离为1或7.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
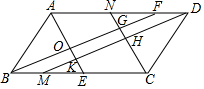 如图,在平行四边形ABCD中,AE,BF,CN,DM分别是∠DAB,∠ABC,∠BCD,∠CDA的角平分线,且相交于点O,K,H,G,求证:四边形HGOK是矩形.
如图,在平行四边形ABCD中,AE,BF,CN,DM分别是∠DAB,∠ABC,∠BCD,∠CDA的角平分线,且相交于点O,K,H,G,求证:四边形HGOK是矩形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com