利用方程、不等式(组)解应用题:
(1)甲每小时走3公里,出发1小时后,乙骑车要在40分钟内追上甲,问乙至少要骑多快才能追上甲?
(2)一批零件共840个,如果甲先做4天,乙再加入合作,则再做8天完成;如果乙先做4天,甲再加入合作,则再做9天完成,问两人每天各做多少个?
(3)某校准备组织290名学生进行野外考察活动,行李共有100件,学校计划租用甲、乙两种型号的汽车共8辆,经了解,甲种汽车每辆最多能载40人和10件行李;乙种汽车每辆最多能载30人和20件行李.
①设租用甲种汽车x辆,请你帮助学校设计所有可能的租车方案;
②如果甲、乙两种汽车每辆的租车费分别为2000元和1800元,请你选择最省钱的租车方案.
分析:(1)属于追及问题,乙路程≥甲路程,需注意甲用的时间为:1+
,乙用是时间为:
;
(2)两个等量关系:甲工效×(4+8)+乙工效×8=840;甲工效×9+乙工效×(4×9)=840;
(3)应列不等式组来进行解答:总人数≥290,总行李数≥100.
解答:解:(1)设:乙的速度为x千米/时,则
x≥3×(1+
)
解得x≥7.5
答:乙至少要骑7.5公里/小时才能追上甲.
(2)设甲每天做x个,乙每天做y个.则
| | (4+8)x+8y=840 | | 9x+(4+9)y=840 |
| |
解得:
答:甲每天做50个,乙每天做30个.
(3)
| | 40x+30×(8-x)≥290 | | 10x+20×(8-x)≥100 |
| |
解得:5≤x≤6
∴第一种是租用甲种汽车5辆,乙种汽车3辆;第二种是租用甲种汽车6辆,乙种汽车2辆;
5×2000+1800×3=15400元
6×2000+1800×2=15600元
15400<15600
第一种租车方案更省费用.
点评:当题中出现至多或至少之类的词语时应用不等式求解.解题关键是要读懂题目的意思,根据题目给出的条件,找出所求的量的合适的等量关系.



 字词句段篇系列答案
字词句段篇系列答案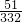 .求我国严重缺水城市有多少座?
.求我国严重缺水城市有多少座?