
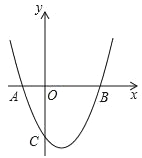
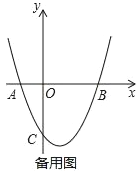
����Ŀ����ƽ��ֱ������ϵxOy�У�������y=x2+bx+c��x�ύ�ڵ�A��B��A��B����ࣩ�������ߵĶԳ���Ϊֱ��x=1��AB=4��
��1���������ߵı���ʽ��
��2����������������M��x1��y1����N��x2��y2������x1��1��x2��1��x1+x2��2�����ж�y1��y2�Ĵ�С����˵�����ɣ�
��3��ƽ�Ƹ������ߣ�ʹƽ�ƺ�������߾�����O������x�ύ�ڵ�D����ƽ�ƺ�������߶���Ϊ��P
������ODP�ǵ���ֱ�������Σ����P�����ꣻ
���ڢٵ������£�ֱ��x=m��0��m��3���ֱ��߶�BP��BC�ڵ�E��F���ҡ�BEF���������BPC�����=2��3��ֱ��д��m��ֵ��
���𰸡���1��y=x2��2x��3����2��y1��y2����3��m��ֵΪ1��3��2![]() ��
��
����������������1���ȸ��������ߺ�x��Ľ��㼰�߶εij�����������ߵĽ���ʽ��
��2�����������ߵĽ���ʽ�жϳ���M��N�Ĵ��λ�ã��ٸ��ݵ�M��N�ĺ�����ķ�Χ�жϺ���ֵ�Ĵ�С���ɣ�
��3������PH��x����H�����ݵ��������ε����ʵõ�PH=OH=OD���������Ϊ������D��x����������ϣ�����D��x��ĸ������ϣ����P���������⼴�ɣ�
�ڵ���D��x����������ϣ��ӳ�HP��BC��Q�����ݴ���ϵ�������ֱ��BP�Ľ���ʽ��ֱ��BC�Ľ���ʽ��Ȼ�������BEF���������BPC�����=2��3�����m��ֵ������D��x��ĸ������ϣ��ӳ�HP��BC��Q��ͬ�����ֱ��BP�Ľ���ʽ��ͬ�����m��ֵ.
��⣺��1���������ߵĶԳ���Ϊֱ��x=1��AB=4��
��A����1��0����B��3��0����
�������߽���ʽΪy=��x+1����x��3����
��y=x2��2x��3��
��2��y1��y2���������£�
��x1��1��x2��1��
��M��N�ڶԳ�������࣬
��x1+x2��2��
��x2��1��1��x1��
���N��ֱ��x=1�ľ����M�㵽ֱ��x=1�ľ���Զ��
��y1��y2��
��3������PH��x����H��
�ߡ�OPDΪ����ֱ�������Σ�
��PH=OH=OD��
����D��x����������ϣ���ͼ1��
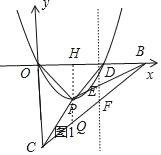
��P��m����m������D��2m��0����
�������ߵĽ���ʽΪy=x��x��2m����
��P��m����m�������m��m��2m��=��m�����m1=0����ȥ����m2=1����P��1����1����
����D��x��ĸ������ϣ���ͼ2��
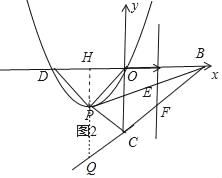
��P��m��m������D��2m��0����
�������ߵĽ���ʽΪy=x��x��2m����
��P��m��m�������m��m��2m��=m�����m1=0����ȥ����m2=��1����P����1����1����
����������P��������1����1����1����1����
�ڵ���D��x����������ϣ���ͼ1���ӳ�HP��BC��Q��
��ֱ��BP�Ľ���ʽΪy=px+q��
��B��3��0����P��1����1�������![]() �����
�����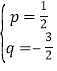 ��
��
��ֱ��BP�Ľ���ʽΪy=![]() x��
x��![]() ��
��
��ֱ��BC�Ľ���ʽΪy=x��3��
��Q��1����2����E��m��![]() m��
m��![]() ����F��m��m��3����
����F��m��m��3����
S��PBC=![]() ��1��3=
��1��3=![]() ��
��
�ߡ�BEF���������BPC�����=2��3��
��S��BEF=1��
��![]() ����
����![]() m+
m+![]() ����3��m��=1�����m1=5����ȥ����m2=1��
����3��m��=1�����m1=5����ȥ����m2=1��
����D��x��ĸ������ϣ���ͼ2���ӳ�HP��BC��Q��
ͬ���ɵ�ֱ��BP�Ľ���ʽΪy=![]() x��
x��![]() ��
��
��Q����1����4����E��m��![]() m��
m��![]() ����F��m��m��3����
����F��m��m��3����
S��PBC=![]() ��3��3=
��3��3=![]() ��
��
�ߡ�BEF���������BPC�����=2��3��
��S��BEF=3��
��![]() ����
����![]() m+
m+![]() ����3��m��=3�����m1=3+2
����3��m��=3�����m1=3+2![]() ����ȥ����m2=3��2
����ȥ����m2=3��2![]() ��
��
����������m��ֵΪ1��3��2![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ô�С��ȵ�С�����ΰ�һ������ƴ������ͼ��.
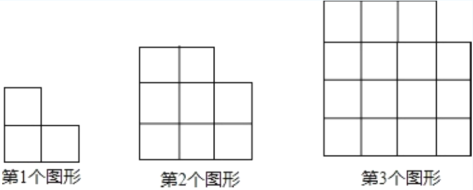
�ŵ�4��ͼ����С�����εĸ�����______��
�Ƶ�![]() ��ͼ����С�����εĸ����Ƕ��٣�
��ͼ����С�����εĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����װ����״��С����ͬ���ĸ�С��ÿ��С���ϸ�����һ�����֣��ֱ���1��4��7��8���ֹ涨�Ӵ�����ȡһ��С��Ӧ��������Ϊһ����λ���ĸ�λ����Ȼ��С��Żش��в�������ȣ�����ȡһ��С��Ӧ��������Ϊ�����λ����ʮλ����
��1��д���������涨�õ����п��ܵ���λ����
��2������Щ��λ������ȡһ������������ƽ��������4��С��7�ĸ��ʣ�
���𰸡���1��16�ֵȿ��ܵĽ�����������ǣ�11��41��71��81��14��44��74��84��17��47��77��87��18��48��78��88����2��![]()
����������1������״ͼ��

����16�ֵȿ��ܵĽ�����������ǣ�11��41��71��81��14��44��74��84��17��47��77��87��18��48��78��88��
��2������ƽ��������4��С��7�Ľ����Ϊ6��
��������ƽ��������4��С��7�ĸ���=![]() =3/8��
=3/8��
�����͡������
��������
23
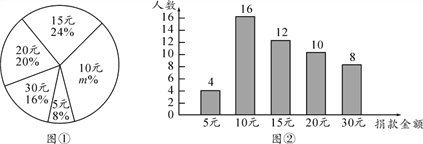
����Ŀ��ij��Уѧ������ȫУ2900��ѧ�������ˡ�����һ�վ衱�����Ϊ�˽��������ѧ������������˲���ѧ���ľ������õõ������ݻ���������ͳ��ͼ�ٺ�ͼ�ڣ�����������Ϣ������������⣺
(1)���ν���������������ѧ������Ϊ____��ͼ����m��ֵ��____��
(2)��������ȡ���������ݵ�ƽ��������������λ����
(3)�����������ݣ����Ƹ�У���λ�����Ϊ10Ԫ��ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������30���ǵ�ֱ�����dz�ABC�Ƶ�B˳ʱ����ת150����õ���EBD������CD����AB=4cm������BCD�����Ϊ��������
A. 4![]() B. 2
B. 2![]() C. 3 D. 2
C. 3 D. 2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() Ϊ�������Σ�
��������![]() ��
��![]() �Ľ�ƽ���ߣ�
�Ľ�ƽ���ߣ�![]() Ҳ���������Σ����н��ۣ���
Ҳ���������Σ����н��ۣ���![]() ����
����![]() ����
����![]() ��������ȷ����________������ţ�.
��������ȷ����________������ţ�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
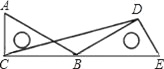
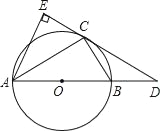
����Ŀ����ͼ����֪��O����ABC�����Բ��AB����O��ֱ����D��AB�ӳ�����һ�㣬AE��DC��DC���ӳ����ڵ�E����ACƽ����EAB��
��1����֤��DE����O�����ߣ�
��2����AB=6��AE=![]() ����BD��BC�ij���
����BD��BC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
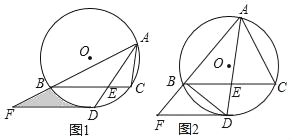
����Ŀ����ͼ1����ABC�ڽ�����O����BAC��ƽ���߽���O�ڵ�D����BC�ڵ�E��BE��EC������BD=2![]() ������D��DF��BC����AB���ӳ����ڵ�F��
������D��DF��BC����AB���ӳ����ڵ�F��
��1����֤��DFΪ��O�����ߣ�
��2������BAC=60����DE=![]() ����ͼ����Ӱ���ֵ������
����ͼ����Ӱ���ֵ������
��3����![]() ��DF+BF=8����ͼ2����BF�ij���
��DF+BF=8����ͼ2����BF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�D��E��F�ֱ��Ǹ��ߵ��е㣬BH��AC���ϵĸߣ�

��1����֤���ı���DBEF��ƽ���ı��Σ���2����֤����DFE����DHE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������˹�ͬ����һ����ʽ����x+a����2x+b�������ڼ׳�����a�ķ��ţ��õ��Ľ����2x2-7x+3����©���˵ڶ�������ʽ��x��ϵ�����õ��Ľ����x2+2x-3��
��1����a��b��ֵ����2���������������ȷ���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com