解:(1)∵a=1,b=m-3,c=-3m,
∴△=(m-3)
2-4×1×(-3m)
=m
2+6m+9
=(m+3)
2≥0,
∴关于x的一元二次方程x
2+(m-3)x-3m=0一定有两个实数根;
(2)∵a=1,b=-2
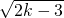
,c=3k-6,
∴△=(-2
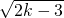
)
2-4×1×(3k-6)
=8k-12-12k+24
=-4k+12,
∵关于x的方程x
2-2
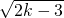
x+3k-6=0有两个不相等的实数根,
∴△=-4k+12>0,
解得:k<3;
∵2k-3≥0,
∴k≥

,
∴

≤k<3;
(3)∵x
2+(m-3)x-3m=0,
∴(x+m)(x-3)=0,
解得:x
1=-m,x
2=3,
∴a=-m,b=3,
∵k为整数,
∴k=2,
若k
2+a
2=b
2,
即4+(-m)
2=9,
∴m=±

,
∵a=-m>0,
∴m<0,
∴m=-

,
若k
2+b
2=a
2,
则4+9=(-m)
2,
解得m=±

,
∵m<0,
∴m=-

,
∴m的值为-

或-

.
分析:(1)根据根的判别式与一元二次方程的关系,可得△≥0,即可证得关于x的一元二次方程x
2+(m-3)x-3m=0一定有两个实数根;
(2)由关于x的方程x
2-2
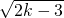
x+3k-6=0有两个不相等的实数根,可得△>0,用含k的代数式表示出△,解不等式即可;
(3)首先表示出a,b,k,再由直角三角形需要满足勾股定理,根据关系式求解即可.
点评:此题考查了根的判别式(当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程没有实数根),以及用因式分解法解一元二次方程.题目难度中等,解题时要注意分析问题要全面.

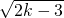 x+3k-6=0有两个不相等的实数根,求k的取值范围;
x+3k-6=0有两个不相等的实数根,求k的取值范围;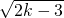 ,c=3k-6,
,c=3k-6,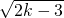 )2-4×1×(3k-6)
)2-4×1×(3k-6)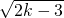 x+3k-6=0有两个不相等的实数根,
x+3k-6=0有两个不相等的实数根, ,
, ≤k<3;
≤k<3; ,
, ,
, ,
, ,
, 或-
或- .
.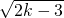 x+3k-6=0有两个不相等的实数根,可得△>0,用含k的代数式表示出△,解不等式即可;
x+3k-6=0有两个不相等的实数根,可得△>0,用含k的代数式表示出△,解不等式即可;

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案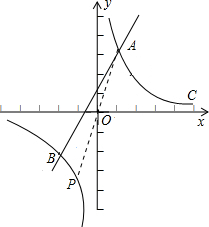 (2010•资阳)如图,已知直线l:y=kx+b与双曲线C:y=
(2010•资阳)如图,已知直线l:y=kx+b与双曲线C:y=