练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．下列四个实数中，最小的实数是（　　）
    A．-2B．2C．-4D．-1

    分析 根据选项中的数据，可以比较它们的大小，从而可以解答本题．

    解答 解：∵-4＜-2＜-1＜2，
    故选C．

    点评 本题考查实数大小的比较，解答此类问题的关键是明确负数小于0小于正数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    1．已知抛物线y=ax2（a＞0）过A（-2，y1）、B（1，y2）两点，则下列关系式一定正确的是（　　）
    A．y1＞0＞y2B．y2＞0＞y1C．y1＞y2＞0D．y2＞y1＞0

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

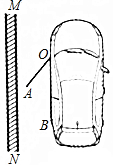    2．如图是一辆小汽车与墙平行停放的平面示意图，汽车靠墙一侧OB与墙MN平行且距离为0.8米．已知小汽车车门宽AO为1.2米，当车门打开角度∠AOB为40°时，车门是否会碰到墙？请说明理由．（参考数据：sin40°≈0.64；cos40°≈0.77；tan40°≈0.84）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．解方程组$\left\{\begin{array}{l}{x+y=5}\\{2x+3y=11}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．若一组数据2，3，x，5，7的众数为7，则这组数据的中位数为（　　）
    A．2B．3C．5D．7

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．为了更好治理闽江水质，保护环境，市治污公司决定购买10台污水处理设备．现有A，B两种型号的设备，其中每台的价格，月处理污水量如下表：
    A型B型
    价格（万元/台）ab
    处理污水量（吨/月）240200
    经调查：购买一台A型设备比购买一台B型设备多2万元，购买2台A型设备和3台B型设备共49万元．
    （1）求a，b的值．
    （2）经预算：市治污公司购买污水处理设备的资金不超过106万元，且该月要求处理闽江的污水量不低于2240吨，你认为该公司有哪几种购买方案，分别为哪几种？
    （3）在（2）的条件下，为了节约资金，请你为治污公司设计一种最省钱的购买方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．已知：3a=9，3b=27，则3a+b+1的值为729．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

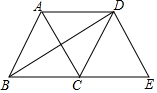    5．如图，等边△ABC沿射线BC向右平移到△DCE的位置，连接AD、BD，则下列结论：①AD=BC；②BD、AC互相平分；③四边形ACED是菱形；④BD=BE．其中正确的个数是（　　）
    A．0B．1C．2D．3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．阅读与思考：
       婆罗摩笈多是一位印度数学家和天文学家，书写了两部关于数学和天文学的书籍，他的一些数学成就在世界数学史上有较高的地位，他的负数及加减法运算仅晚于中国九章算术而他的负数乘除法法则在全世界都是领先的，他还提出了著名的婆罗摩笈多定理，该定理的内容及部分证明如下：
        已知：如图，四边形ABCD内接于圆O，对角线AC⊥BD于点M，ME⊥BC于点E，延长EM交CD于点F，求证：F是AD中点
     证明∵AC⊥BD，ME⊥BC
    ∴∠CBD=∠CME
    ∵∠CBD=∠CAD，∠CME=∠AMF
    ∴∠CAD=∠AMF
    ∴AF=MF
    ∵∠AMD=90°，同时∠MAD+∠MDA=90°
    ∴∠FMD=∠FDM
    ∴MF=DF，∴AF=DF即F是AD中点．
    请你阅读婆罗摩笈多定理的证明过程，完成婆罗摩笈多逆定理的证明：
    （1）如图1，四边形ABCD内接于圆O，对角线AC⊥BD于点M，F为AD中点，连接FM并延长交BC于点E，求证：ME⊥BC．
    （2）已知：如图2，△ABC内接于圆O，∠B=30°，∠ACB=45°，AB=2，点D在圆O上，∠BCD=60°，连接AD交BC于点P，作ON⊥CD于点N，连接并延长NP交AB于点M，求证PM⊥BA并求PN的长．

    查看答案和解析>>

    同步练习册答案