
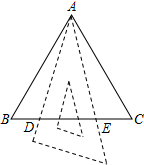
 如图,△ABC是边长为a的等边三角形,将三角板的30°角的顶点与A重合,三角板30°角的两边与BC交于D、E两点,则DE长度的取值范围是(2$\sqrt{3}$-3)a≤DE≤$\frac{1}{2}$a..
如图,△ABC是边长为a的等边三角形,将三角板的30°角的顶点与A重合,三角板30°角的两边与BC交于D、E两点,则DE长度的取值范围是(2$\sqrt{3}$-3)a≤DE≤$\frac{1}{2}$a.. 分析 当B、D重合或C、E重合时DE长度最大,解直角三角形即可求得DE的最大值;当∠BAD=∠CAE=15°时,DE长度最小,作AF⊥BC,且AF=AB,连接DF、CF,证明△ABD≌△ADF,则∠B=∠AFD,BD=DF,然后证明△ABH∽△DFH,根据相似三角形的性质求得DH=$\frac{\frac{1}{2}a•\frac{\sqrt{3}}{2}a}{a+\frac{\sqrt{3}}{2}a}$=$\frac{2\sqrt{3}-3}{2}$a,即可求得DE的最小值.
解答 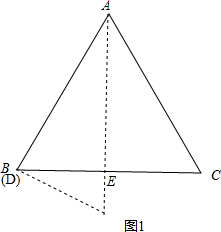 解:当B、D重合或C、E重合时DE长度最大,如图1,
解:当B、D重合或C、E重合时DE长度最大,如图1,
∵∠BAE=30°,∠AEB=90°,
∴DE=$\frac{1}{2}$AB=$\frac{1}{2}$a,
当∠BAD=∠CAE=15°时,DE长度最小,如图2,
作AF⊥BC,且AF=AB,连接DF、CF,
∵AF⊥BC,
∴∠BAF=∠CAF=30°,
∵∠BAD=∠CAE=15°,
∴∠DAH=∠EAH=15°,
∴∠BAD=∠DAH,
在△ADB和△ADF中,
$\left\{\begin{array}{l}{AB=AF}\\{∠BAD=∠DAH}\\{AD=AD}\end{array}\right.$,
∴△ABD≌△ADF,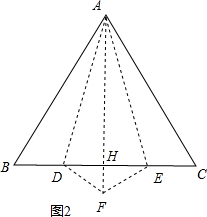
∴∠B=∠AFD,BD=DF,
∵∠AHB=∠DHF=90°,
∴△ABH∽△DFH,
AB:AH=DF:DH,
∴$\frac{AB}{AH}$=$\frac{BD}{DH}$,
∴$\frac{AB+AH}{AH}$=$\frac{BD+DH}{DH}$,
∴DH=$\frac{(BD+DH)•AH}{AB+AH}$,其中BD+DH=$\frac{1}{2}$a、AH=$\frac{\sqrt{3}}{2}$a,
∴DH=$\frac{\frac{1}{2}a•\frac{\sqrt{3}}{2}a}{a+\frac{\sqrt{3}}{2}a}$=$\frac{2\sqrt{3}-3}{2}$a
∴DE=(2$\sqrt{3}$-3)a,
故DE长度的取值范围是(2$\sqrt{3}$-3)a≤DE≤$\frac{1}{2}$a.
点评 本题考查了等边三角形的性质,全等三角形的判定和性质以及相似三角形的和性质,分类讨论思想的运用是解题的关键.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:解答题
 【合作学习】如图,矩形ABOD的两边OB,OD都在坐标轴的正半轴上,OD=3,另两边与反比例函数y=$\frac{k}{x}$(k≠0)的图象分别相交于点E,F,且DE=2.过点E作EH⊥x轴于点H,过点F作FG⊥EH于点G.回答下面的问题:
【合作学习】如图,矩形ABOD的两边OB,OD都在坐标轴的正半轴上,OD=3,另两边与反比例函数y=$\frac{k}{x}$(k≠0)的图象分别相交于点E,F,且DE=2.过点E作EH⊥x轴于点H,过点F作FG⊥EH于点G.回答下面的问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,顺次连结A(-3,-2),B(3,-2),C(1,1),D(-2,1)各点,你会得到一个什么图形?在给定坐标系中画出这个图形求出该图形的面积.
在平面直角坐标系中,顺次连结A(-3,-2),B(3,-2),C(1,1),D(-2,1)各点,你会得到一个什么图形?在给定坐标系中画出这个图形求出该图形的面积.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,AD平分∠BAC,按如下步骤作图:
如图,在△ABC中,AD平分∠BAC,按如下步骤作图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明把一根长160cm的竹条做成一个等腰三角形的风筝的边框(如图),已知该三角形的底边上的高AD=40cm,请问AB、AC、BC的长分别是多少?
小明把一根长160cm的竹条做成一个等腰三角形的风筝的边框(如图),已知该三角形的底边上的高AD=40cm,请问AB、AC、BC的长分别是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com