
【题目】拼图是一种研究代数恒等式的重要方法,所谓的拼图指的是把所给的图形以不同的方式拼成不同形状的图形,把图形面积用不同的代数式表示,由于拼图前后的面积相等,从而相应的代数式的值也相等,进而得到代数恒等式.
(1)智慧学习小组探索了用4个如图1所示的全等的长方形(长、宽分别为a、b)拼成不同的图形.在研究过程中,他们用这4个长方形拼成了一个如图2所示的“回形”正方形.拼图前后,请写出该小组所用图形(4个长方形)的面积的计算方法:拼图前: ;拼图后: ;因为拼图前后的面积不变,所以可得代数恒等式: .

(2)利用(1)中得到的恒等式,解决下面的问题:已知![]() 求xy的值.
求xy的值.
(3)超人学习小组受智慧学习小组的启发,用4个如图3所示的全等的直角三角形(三边长分别为a、b、c)拼成了两种“中空”的正方形.请你画出这两种图形:
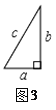
由上面的图形可得代数恒等式: .
(4)利用(3)中得到的代数恒等式,解决下面的问题:在Rt△ABC中,已知∠ABC=90°,AB=6,BC=8,求AC的长.
【答案】(1)4ab,(a+b)2 - (a-b)2,4ab = (a+b)2 - (a-b)2 ;
(2)![]() ;
;
(3)画图见解析,![]()
(4)AC= 10
【解析】(1)通过观察可以得大正方形边长为a+b,小正方形边长为a-b,利用大正方形面积减去小正方形面积即为阴影部分的面积,得出答案;(2)由(1)的结论变形后即可得出xy的值;(3)通过两个组合正方形的面积之间相等的关系即可证明勾股定理;(4)根据勾股定理:在如何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方,即BC2=AC2+AB2,结合BC=10,AB=6,可求出另一条直角边AC的长度.
解:(1)拼图前:4ab
拼图后:(a+b)2 - (a-b)2
观察图形得:
大正方形边长为:a+b,
小正方形边长为:a-b,
根据大正方形面积-小正方形面积=阴影部分面积得:
4ab=(a+b)2-(a-b)2.
可得代数恒等式: 4ab = (a+b)2 - (a-b)2
故答案为:4ab = (a+b)2 - (a-b)2.
“点睛”本题考查了完全平方公式的几何背景,学生需要掌握完全平方公式和几何图形的关系即可,题目整体涉及很好,可以考查学生的观察能力.
(2)由(1)可得,4ab = (a+b)2 - (a-b)2,
∴ 4xy = (x+y)2 - (x-y)2
∴ ![]()
又∵ ![]() ,
,![]()
∴ ![]() ,
,![]()
∴![]() .
.
(3)如图所示,
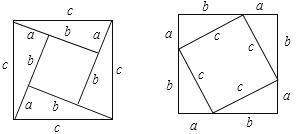
![]()
解:选用(1).
证明:∵S大正方形=c2
S大正方形=4S△+S小正方形=4×![]() ab+(b-a)2,
ab+(b-a)2,
∴c2=4×![]() ab+(b-a)2-c2=a2+b2;
ab+(b-a)2-c2=a2+b2;
选用(2):
证明:图中把大正方形的面积分了四分部,分别是:边长为a的正方形,边长为b的正方形,还有两个长为b,宽为a的长方形.
∵根据面积相等得:(a+b)2=c2+b2+4×![]() ab,
ab,
由右图可得(a+b)2=c2+4×![]() ab,
ab,
∴a2+b2+4×![]() ab=c2+4×
ab=c2+4×![]() ab,
ab,
∴a2+b2=c2.
(4)∵在Rt△ABC中,∠ABC=90°,
∴ ![]() ,
,
又∵ AB=6,BC=8,
∴ ![]() .
.
∴ AC= 10.
“点睛”本题考查利用图形面积的关系证明勾股定理,解题关键是利用三角形和正方形边长关系进行组合图形.像这类直接考查定义的题目,解答的关键是熟练掌握勾股定理的定义及其在直角三角形中的表示形式.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+3上的三点,则y1,y2,y3的大小关系为( )
A. y1>y2>y3 B. y1>y3>y2 C. y3>y2>y1 D. y3>y1>y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好的开展“我爱阅读”活动,小明针对某校七年级学生(共16个班,480名学生)课外阅读喜欢图书的种类(每人只能选一种书籍)进行了调查.
(1)小明采取的下列调查方式中,比较合理的是 ;理由是: .
A.对七年级(1)班的全体同学进行问卷调查;
B.对七年级各班的语文科代表进行问卷调查;
C.对七年级各班学号为3的倍数的全体同学进行问卷调查.
(2)小明根据问卷调查的结果绘制了如下两幅不完整的统计图,根据图中提供的信息解答下列问题:
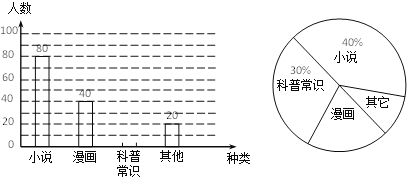
① 在扇形统计图中,“其它”所在的扇形的圆心角等于 度;
② 补全条形统计图;
③ 根据调查结果,估计七年级课外阅读喜欢“漫画”的同学有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处,若∠2=40°,则图中∠1的度数为( )

A. 115° B. 120° C. 130° D. 140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(m﹣2)x﹣m=0.
(1)求证:方程有两个不相等的实数根;
(2)如果方程的两实数根为x1,x2,且x1+x2﹣x1x2=7,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加快城市群的建设与发展,在A,B两城市间新建条城际铁路,建成后,铁路运行里程由现在的120km缩短至114km,城际铁路的设计平均时速要比现行的平均时速快110km,运行时间仅是现行时间的![]() ,求建成后的城际铁路在A,B两地的运行时间.
,求建成后的城际铁路在A,B两地的运行时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以Rt△ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E为OB的中点,连接CE并延长交⊙O于点F,点F恰好落在弧AB的中点,连接AF并延长与CB的延长线相交于点G,连接OF.
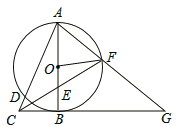
(1)求证:OF=![]() BG;
BG;
(2)若AB=4,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在100个数据中,用适当的方法,抽取50个作为样本进行统计,频数分布表中55~58这一组数据的频率是0.12,那么估计这100个数据中,落在55~58之间的约有( )
A. 120个 B. 60个 C. 12个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AE、BF分别平分∠DAB和∠ABC,交CD于点E、F,AE、BF相交于点M.
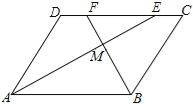
(1)试说明:AE⊥BF;
(2)判断线段DF与CE的大小关系,并予以说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com