
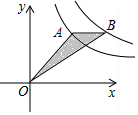
 如图,在直角坐标系中,点A是反比例函数y=$\frac{2}{x}$图象在第一象限上的一点,过点A作x轴的平行线交反比例函数y=$\frac{4}{x}$图象于点B,当点A的横坐标逐渐增大时,则△ABO的面积变化情况是( )
如图,在直角坐标系中,点A是反比例函数y=$\frac{2}{x}$图象在第一象限上的一点,过点A作x轴的平行线交反比例函数y=$\frac{4}{x}$图象于点B,当点A的横坐标逐渐增大时,则△ABO的面积变化情况是( )| A. | 先减小后增大 | B. | 先增大后减小 | C. | 不断增大 | D. | 保持不变 |
分析 根据题意可以分别设出点A和点B的坐标,然后根据它们的纵坐标相等,可以得到横坐标的关系,然后根据三角形的面积计算公式即可求得△ABO的面积,本题得以解决.
解答 解:设点A的坐标为(a,$\frac{2}{a}$),点B的坐标为(b,$\frac{4}{b}$),
∵$\frac{2}{a}=\frac{4}{b}$,
∴b=2a,
∴△ABO的面积是:$\frac{1}{2}(b-a)•\frac{2}{a}$=$\frac{1}{2}(2a-a)•\frac{2}{a}=1$,
∴点A的横坐标逐渐增大时,则△ABO的面积变化情况是保持不变,
故选D.
点评 本题考查反比例函数系数k的几何意义,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想和反比例函数的性质解答.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:填空题
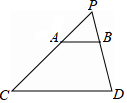 如图,光源P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=6m,点P到CD的距离是2.7m,则AB离地面的距离为1.8m.
如图,光源P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=6m,点P到CD的距离是2.7m,则AB离地面的距离为1.8m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
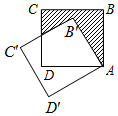 如图,边长为3的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分的面积为( )
如图,边长为3的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分的面积为( )| A. | 6+3$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 1-$\frac{\sqrt{3}}{3}$ | D. | 9-3$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
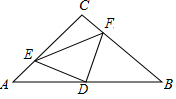 如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,E,F两点分别在AC,BC边上运动 (点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:
如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,E,F两点分别在AC,BC边上运动 (点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com