
如图,在四边形ABCD中,AD<BC,对角线AC、BD相交于O点,AC=BD,∠ACB=∠DBC.
(1)求证:四边形ABCD为等腰梯形.
(2)若E为AB上一点,延长DC至F,使CF=BE,连接EF 交BC于G,请判断G点是否为EF中点,并说明理由. (改编)
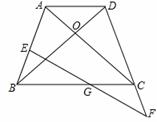
(1)证明:∵∠ACB=∠DBC,∴OB=OC,
∵AC=BD,∴OA=OD,∴∠OAD=∠ODA,
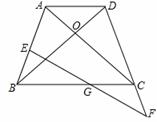 ∵∠DOC=∠OAD+∠ODA=∠OBC+∠OCB,
∵∠DOC=∠OAD+∠ODA=∠OBC+∠OCB,
∴2∠OAD=2∠OCB,∴∠OAD=∠OCB,∴AD∥BC
∵AD<BC,∴四边形ABCD为梯形.(2分)
在△ABC和△DCB中:AC=BD,∠ACB=∠DBC,CB=BC.
∴△ABC≌△DCB,∴AB=CD,(2分)∴四边形ABCD为等腰梯形.(1分)
(2)解:点G是EF中点.(1分)理由:
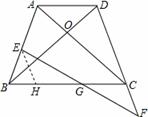 过E作EH∥CD交BC于H.∴∠EHB=∠DCB,∠EHG=∠GCF,
过E作EH∥CD交BC于H.∴∠EHB=∠DCB,∠EHG=∠GCF,
∵梯形ABCD为等腰梯形,∴∠EBH=∠DCB,
∴∠EBH=∠EHB,∴EB=EH,(2分)
∵EB=CF,∴EH=CF,
在△EHG和△FGC中:∠EHG=∠FCG,∠EGH=∠FGC,EH=CF,
∴△EHG≌△FGC,∴EG=FG即G为EF中点.(2分)


科目:初中数学 来源: 题型:
如果一条抛物线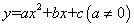 与
与 轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”,[a,b,c]称为“抛物线三角形系数”.
轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”,[a,b,c]称为“抛物线三角形系数”.
(1)若抛物线三角形系数为[-1,b,0]的“抛物线三角形”是等腰直角三角形,求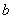 的值;
的值;
(2)若△OAB是“抛物线三角形”,其中点B为顶点,抛物线三角形系数为[-2,2m,0],其中m>0;且四边形ABCD是以原点O为对称中心的矩形,求出过O、C、D三个点的抛物线的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,菱形ABCD的边长为12cm,∠A=60°,点P从点A出发沿线路AB→BD做匀速运动,点Q从点D同时出发沿线路DC→CB→BA做匀速运动.已知点P,Q运动的速度分别为2cm/秒和2.5cm/秒,经过12秒后,P、Q分别到达M、N两点时,点P、Q再分别从M、N同时沿原路返回,点P的速度不变,点Q的速度改为vcm/秒,经过3秒后,P、Q分别到达E、F两点,若△BEF与△AMN相似,则v的值为

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知边长为2的正三角形ABC顶点A的坐标为(0,6),BC的中点D在y轴上,且在点A下方,点E是边长为2,中心在原点的正六边形的一个顶点,把这个正六边形绕中心旋转一周,在此过程中DE的最小值为( )(改编)
| A. | 4 | B. | 4﹣ | C. | 3 | D. | 6﹣2 |
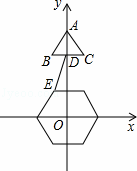
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,直线 与直线
与直线 相交于点
相交于点 .直线
.直线 与y轴交于点A.一动点
与y轴交于点A.一动点 从点A出发,先沿平行于x轴的方向运动,到达直线
从点A出发,先沿平行于x轴的方向运动,到达直线 上的点
上的点 处后,改为垂直于x轴的方向运动,到达直线
处后,改为垂直于x轴的方向运动,到达直线 上的点
上的点 处后,再沿平行于x轴的方向运动,到达直线
处后,再沿平行于x轴的方向运动,到达直线 上的点
上的点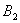 处后,又改为垂直于x轴的方向运动,到达直线
处后,又改为垂直于x轴的方向运动,到达直线 上的点
上的点 处后,仍沿平行于x轴的方向运动,…… 照此规律运动,动点
处后,仍沿平行于x轴的方向运动,…… 照此规律运动,动点 依次经过点
依次经过点 ,
, ,
,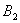 ,
, ,
,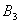 ,
, ,…,
,…, ,
, ,…
,…
则当动点 到达
到达 处时,运动的总路径的长为( )(根据2011江干区模拟改编)
处时,运动的总路径的长为( )(根据2011江干区模拟改编)
A.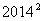 B.
B. C.
C. D.
D.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图①,有6张写有实数的卡片,它们的背面都相同,现将它们背面朝上洗匀后如图②摆放,从中任意翻开两张都是无理数的概率是( )
(A)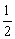 (B)
(B)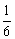 (C)
(C)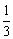 (D)
(D)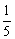
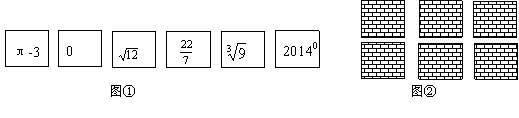

查看答案和解析>>
科目:初中数学 来源: 题型:
小明家今年种植的“红灯”樱桃喜获丰收,采摘上市20天全部销售完,小明对销售情况进行了跟踪记录,并将记录情况绘成图象,日销售量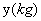 与上市时间
与上市时间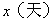 的函数关系如图1所示,樱桃价格
的函数关系如图1所示,樱桃价格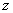 (元/
(元/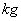 )与上市时间
)与上市时间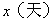 的函数关系式如图2所示。
的函数关系式如图2所示。
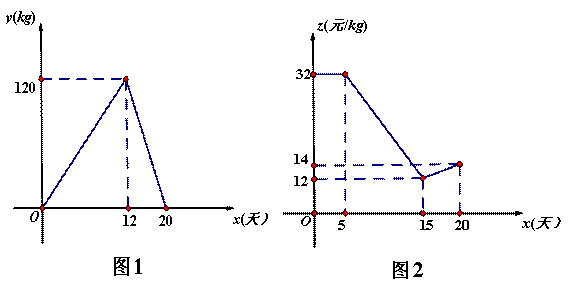 |
(1)求小明家樱桃的日销售量y与上市时间x的函数解析式。
(2)求当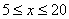 时,樱桃的价格z与上市时间x的函数解析式。
时,樱桃的价格z与上市时间x的函数解析式。
(3)求哪一天的销售金额达到最大,最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com