
【题目】在平面直角坐标系中,若要把一条直线平移到某个位置,经常可通过方式一:上(下)平移,或者方式二:左(右)平移的其中一种达到目的.现有直线![]() 交
交![]() 轴于点
轴于点![]() ,若把直线
,若把直线![]() 向右平移8个单位长度得到直线
向右平移8个单位长度得到直线![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)求直线![]() 的解析式,并说明直线
的解析式,并说明直线![]() 若按方式一是如何平移到直线
若按方式一是如何平移到直线![]() 的位置;
的位置;
(2)若直线![]() 上的一点
上的一点![]() ,点
,点![]() 按方式一平移后在直线
按方式一平移后在直线![]() 上的对应点记为点
上的对应点记为点![]() .
.
①若点![]() 在直线
在直线![]() 上,且
上,且![]() ,求点
,求点![]() 的坐标(用含
的坐标(用含![]() 的式子表示) ;
的式子表示) ;
②当![]() 时,试证明直线
时,试证明直线![]() 必将四边形
必将四边形![]() 的面积二等分.
的面积二等分.

【答案】(1)![]() ,向上平移4个单位;(2)①点
,向上平移4个单位;(2)①点![]() 的坐标为
的坐标为![]() ;②证明见解析
;②证明见解析
【解析】
(1)根据直线平行k相等,可求直线![]() 的解析式,根据两直线与x轴交点坐标可确定按方式一是如何平移到直线
的解析式,根据两直线与x轴交点坐标可确定按方式一是如何平移到直线![]() 的;
的;
(2)①根据B在直线![]() 上可得
上可得![]() ,由B的对应点为C,可得点C
,由B的对应点为C,可得点C![]() ,且BC∥y轴,由中点坐标公式可得中点坐标,根据线段垂直平分线的性质得点P在BC的垂直平分线上,即点P的纵坐标和BC中点的纵坐村都是
,且BC∥y轴,由中点坐标公式可得中点坐标,根据线段垂直平分线的性质得点P在BC的垂直平分线上,即点P的纵坐标和BC中点的纵坐村都是![]() ,设点P的横坐标为
,设点P的横坐标为![]() ,代入可得结论;
,代入可得结论;
②证明四边形ABCD是平行四边形,连接BD、AC,交点记为点E,确定E![]() ,则过点E的直线把平行四边形ABCD的面积二等分,再证明直线直线
,则过点E的直线把平行四边形ABCD的面积二等分,再证明直线直线![]() 必过E点,可得结论.
必过E点,可得结论.
解:(1)![]() ,
,
当![]() 时,
时,![]() ,
,
∴直线![]() 与
与![]() 轴交点坐标为
轴交点坐标为![]() ,
,
按方式二平移后的对应点为![]() ,且在直线
,且在直线![]() 上,
上,
设直线![]() 的解析式为
的解析式为![]()
∴![]() ,
,
∴直线![]() 的解析式为:
的解析式为:![]() ,
,
![]() ,
,
∴直线![]() 若按方式一向上平移4个单位得到直线
若按方式一向上平移4个单位得到直线![]() ;
;
(2)①如图1,∵点![]() 在直线
在直线![]() 上,
上,
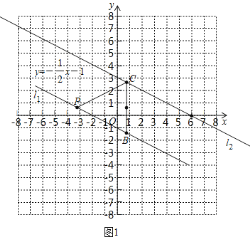
![]() ,
,
∴点![]() ,
,
由(1)得,点![]() ,且
,且![]() 轴,
轴,
∴![]() 的中点坐标为
的中点坐标为![]() ,
,
![]()
∴点![]() 在
在![]() 的垂直平分线上,
的垂直平分线上,
又∵![]() 轴,
轴,
∴点![]() 的纵坐标为
的纵坐标为![]() ,
,
设点![]() 的横坐标为
的横坐标为![]() ,
,
![]() ,
,
![]()
∴点![]() 的坐标为
的坐标为![]() ;
;
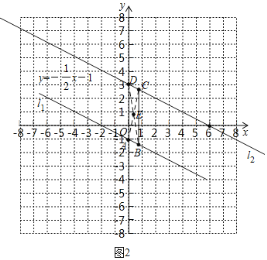
②如图2,根据题意得:![]() ,
,![]() ,
,![]()
![]() ,
,
由平移可知![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
连接四边形![]() 的对角线,交点记为点
的对角线,交点记为点![]() ,则
,则![]() 是
是![]() 的中点,
的中点,
![]() ,
,
![]()
![]() 过点
过点![]() 的直线把平行四边形
的直线把平行四边形![]() 的面积二等分,
的面积二等分,
把![]() 代入
代入![]() 中,得
中,得![]() ,
,
即当![]() 时,直线
时,直线![]() 必过
必过![]() 点,
点,
直线![]() 必将四边形
必将四边形![]() 的面积二等分.
的面积二等分.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】一副含 ![]() 和
和 ![]() 角的三角板
角的三角板 ![]() 和
和 ![]() 叠合在一起,边
叠合在一起,边 ![]() 与
与 ![]() 重合,
重合, ![]() (如图1),点
(如图1),点 ![]() 为边
为边 ![]()
![]() 的中点,边
的中点,边 ![]() 与
与 ![]() 相交于点
相交于点 ![]() ,此时线段
,此时线段 ![]() 的长是 . 现将三角板
的长是 . 现将三角板 ![]() 绕点
绕点 ![]() 按顺时针方向旋转(如图2),在
按顺时针方向旋转(如图2),在 ![]() 从
从 ![]() 到
到 ![]() 的变化过程中,点
的变化过程中,点 ![]() 相应移动的路径长共为 . (结果保留根号)
相应移动的路径长共为 . (结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E、F是AC上的点,判断下列说法错误的是( ) 
A.若EF⊥AC,则EF是⊙O的切线
B.若EF是⊙O的切线,则EF⊥AC
C.若BE=EC,则AC是⊙O的切线
D.若BE= ![]() EC,则AC是⊙O的切线
EC,则AC是⊙O的切线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人因需要经常去复印资料,甲复印社按A4纸每10页2元计费,乙复印社则按A4纸每10页0.8元计费,但需按月付一定数额的承包费.两复印社每月收费情况如图所示,根据图中提供的信息解答下列问题:
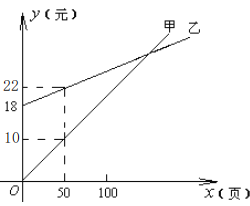
(1)乙复印社要求客户每月支付的承包费是_______元;
(2)当每月复印_______页时,两复印社实际收费相同;
(3)如果每月复印200页时,应选择_______复印社?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB和CD相交于点O,在∠COB的内部作射线OE.
(1)若∠AOC=36°,∠COE=90°,求∠BOE的度数;
(2)若∠COE:∠EOB:∠BOD=4:3:2,求∠AOE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程(k-2)x2-4x+2=0有两个不相等的实数根.
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程x2-4x+k=0与x2+mx-1=0有一个相同的根,求此时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器经营业主计划购进一批同种型号的冷风扇和普通电风扇,若购进8台冷风扇和20台普通电风扇,需要资金17400元,若购进10台冷风扇和30台普通电风扇,需要资金22500元.求冷风扇和普通电风扇每台的采购价各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江南农场收割小麦,已知1台大型收割机和3台小型收割机1小时可以收割小麦1.4公顷,2台大型收割机和5台小型收割机1小时可以收割小麦2.5公顷.
(1)每台大型收割机和每台小型收割机1小时收割小麦各多少公顷?
(2)大型收割机每小时费用为300元,小型收割机每小时费用为200元,两种型号的收割机一共有10台,要求2小时完成8公顷小麦的收割任务,且总费用不超过5400元,有几种方案?请指出费用最低的一种方案,并求出相应的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】茜茜受《乌鸦喝水》故事的启发,利用量筒、大球和小球进行了如下操作,请根据图中给出的信息,解答下列问题:
(1)放入一个小球水面升高______cm,放入一个大球水面升高______cm.
(2)如果要使水面上升到50cm,应放入大球、小球各多少个?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com