
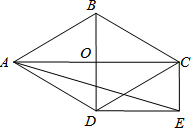
 如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.
如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.分析 (1)根据平行四边形的判定得出边形OCED是平行四边形,根据菱形的性质求出∠COD=90°,根据矩形的判定得出即可;
(2)解直角三角形求出AO、DO、求出AC、CE,根据勾股定理求出AE,解直角三角形求出即可.
解答 (1)证明:∵DE∥AC,CE∥BD,
∴DE∥OC,CE∥OD,
∴四边形OCED是平行四边形,
又∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠COD=90°,
∴四边形OCED是矩形;
(2)解:∵∠ADB=60°,AD=2$\sqrt{3}$,
∴OD=$\sqrt{3}$,AO=3,
∴CE=$\sqrt{3}$,AC=6,
由勾股定理得:AE=$\sqrt{A{C}^{2}+C{E}^{2}}$=$\sqrt{{6}^{2}+(\sqrt{3})^{2}}$=$\sqrt{39}$,
∴sin∠AED=sin∠CAE=$\frac{CE}{AE}$$\frac{\sqrt{3}}{\sqrt{39}}$=$\frac{\sqrt{13}}{13}$.
点评 本题考查了菱形的性质,矩形的判定,平行四边形的判定和性质,勾股定理的应用,能综合运用知识点进行推理是解此题的关键,注意:菱形的对角线互相平分且垂直.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:解答题
 大商超市为了吸引顾客,设立了一个抽奖活动.如图,活动规则:顾客单票(每次)购物满100元,就能获得一次抽奖机会,且百分之百中奖.顾客同时掷分别标有数字1至6的两个骰子,数字朝上的点数之和是几,就能获得相应数字格子中的物品.
大商超市为了吸引顾客,设立了一个抽奖活动.如图,活动规则:顾客单票(每次)购物满100元,就能获得一次抽奖机会,且百分之百中奖.顾客同时掷分别标有数字1至6的两个骰子,数字朝上的点数之和是几,就能获得相应数字格子中的物品.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | -1 | 0 | 1 |
| ax2 | -- | -- | 1 |
| ax2+bx+c | 7 | 2 | -- |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 4 | B. | 2$\sqrt{3}$ | C. | 12 | D. | 4$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com