
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)求证:该方程有两个实数根;
(2)若该方程的两个实数根![]() 、
、![]() 满足
满足![]() ,求
,求![]() 的值.
的值.
 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】材料一:一个正整数x能写成x=a2﹣b2(a,b均为正整数,且a≠b),则称x为“雪松数”,a,b为x的一个平方差分解,在x的所有平方差分解中,若a2+b2最大,则称a,b为x的最佳平方差分解,此时F(x)=a2+b2.
例如:24=72﹣52,24为雪松数,7和5为24的一个平方差分解,32=92﹣72,32=62﹣22,因为92+72>62+22,所以9和7为32的最佳平方差分解,F(32)=92+72
材料二:若一个四位正整数,它的千位数字与个位数字相同,百位数字与十位数字相同,但四个数字不全相同,则称这个四位数为“南麓数”.例如4334,5665均为“南麓数”.
根据材料回答:
(1)请直接写出两个雪松数,并分别写出它们的一对平方差分解;
(2)试证明10不是雪松数;
(3)若一个数t既是“雪松数”又是“南麓数”,并且另一个“南麓数”的前两位数字组成的两位数与后两位数字组成的两位数恰好是t的一个平方差分解,请求出所有满足条件的数t中F(t)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
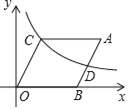
【题目】如图,ABOC放置在直角坐标系中,点A(10,4),点B(6,0),反比例函数y=![]() (x>0)的图象经过点C.
(x>0)的图象经过点C.
(1)求该反比例函数的表达式.
(2)记AB的中点为D,请判断点D是否在该反比例函数的图象上,并说明理由.
(3)若P(a,b)是反比例函数y=![]() 的图象(x>0)的一点,且S△POC<S△DOC,则a的取值范围为_____.
的图象(x>0)的一点,且S△POC<S△DOC,则a的取值范围为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
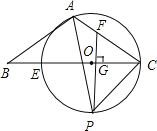
【题目】如图,在△ABC 中,AB=AC,∠BAC=120°,E 为 BC 上一点,以 CE 为直径作⊙O 恰好经过 A、C 两点, PF⊥BC 交 BC 于点 G,交 AC 于点 F.
(1)求证:AB 是⊙O 的切线;
(2)如果 CF =2,CP =3,求⊙O 的直径 EC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列是幼儿园小朋友用火柴棒拼出的一列图形.

仔细观察,找出规律,解答下列各题:
(1)第4个图中共有______根火柴,第6个图中有______根火柴;
(2)第![]() 个图形中共有______根火柴(用含
个图形中共有______根火柴(用含![]() 的式子表示);
的式子表示);
(3)请计算第2008个图形中共有多少根火柴?
查看答案和解析>>
科目:初中数学 来源: 题型:
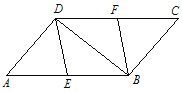
【题目】如图,在□ABCD 中,∠ADB=90°,点 E 为 AB 边的中点,点 F 为CD 边的中点.
(1)求证:四边形 DEBF 是菱形;
(2)当∠A 等于多少度时,四边形 DEBF 是正方形?并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() (k为常数,k≠0)的图象经过点A(2,3).
(k为常数,k≠0)的图象经过点A(2,3).
(1)求这个函数的解析式;
(2)判断点B(-1,6),C(3,2)是否在这个函数的图象上,并说明理由;
(3)当-3<x<-1时,求y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
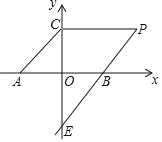
【题目】如图,直线y=x+3与x轴、y轴分别相交于A、C两点,过点B(6,0),E(0,﹣6)的直线上有一点P,满足∠PCA=135°.
(1)求证:四边形ACPB是平行四边形;
(2)求直线BE的解析式及点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com