
【题目】如图,在平面直角坐标系xOy中,A(0,5),直线x=-5与x轴交于点D,直线y=-![]() x-
x-![]() 与x轴及直线x=-5分别交于点C,E.点B,E关于x轴对称,连接AB.
与x轴及直线x=-5分别交于点C,E.点B,E关于x轴对称,连接AB.
(1)求点C,E的坐标及直线AB的解析式;
(2)若S=S△CDE+S四边形ABDO,求S的值;
(3)在求(2)中S时,嘉琪有个想法:“将△CDE沿x轴翻折到△CDB的位置,而△CDB与四边形ABDO拼接后可看成△AOC,这样求S便转化为直接求△AOC的面积,如此不更快捷吗?”但大家经反复验算,发现S△AOC≠S,请通过计算解释他的想法错在哪里.
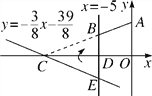
【答案】(1)C(-13,0),E(-5,-3),![]() ;(2)32;(3)见解析.
;(2)32;(3)见解析.
【解析】
(1)利用坐标轴上点的特点确定出点C的坐标,再利用直线的交点坐标的确定方法求出点E坐标,进而得到点B坐标,最后用待定系数法求出直线AB解析式;
(2)直接利用直角三角形的面积计算方法和直角梯形的面积的计算即可得出结论,
(3)先求出直线AB与x轴的交点坐标,判断出点C不在直线AB上,即可.
(1)在直线![]() 中,令y=0,则有0=
中,令y=0,则有0=![]() ,
,
∴x=﹣13,
∴C(﹣13,0),
令x=﹣5,代入![]() ,解得y=﹣3,
,解得y=﹣3,
∴E(﹣5,﹣3),
∵点B,E关于x轴对称,
∴B(﹣5,3),
∵A(0,5),
∴设直线AB的解析式为y=kx+5,
∴﹣5k+5=3,
∴k=![]() ,
,
∴直线AB的解析式为![]() ;
;
(2)由(1)知E(﹣5,﹣3),
∴DE=3,
∵C(﹣13,0),
∴CD=﹣5﹣(﹣13)=8,
∴S△CDE=![]() CD×DE=12,
CD×DE=12,
由题意知,OA=5,OD=5,BD=3,
∴S四边形ABDO=![]() (BD+OA)×OD=20,
(BD+OA)×OD=20,
∴S=S△CDE+S四边形ABDO=12+20=32;
(3)由(2)知,S=32,
在△AOC中,OA=5,OC=13,
∴S△AOC=![]() OA×OC=
OA×OC=![]() =32.5,
=32.5,
∴S≠S△AOC,
理由:由(1)知,直线AB的解析式为![]() ,令y=0,则0=
,令y=0,则0=![]() ,
,
∴x=﹣![]() ≠﹣13,
≠﹣13,
∴点C不在直线AB上,
即:点A,B,C不在同一条直线上,
∴S△AOC≠S.


科目:初中数学 来源: 题型:
【题目】如图,点E在正方形ABCD的边AB上,连接DE,过点C作CF⊥DE于F,过点A作AG∥CF交DE于点G.
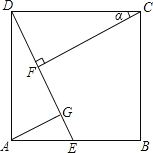
(1)求证:△DCF≌△ADG.
(2)若点E是AB的中点,设∠DCF=α,求sinα的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
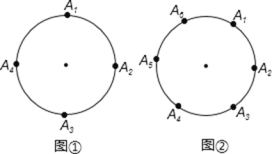
【题目】如图①,如果 A1、A2、A3、A4 把圆周四等分,则以A1、A2、A3、A4为顶点的直角三角形4个;如图②,如果A1、A2、A3、A4、A5、A6 把圆周六等分,则以A1、A2、A3、A4、A5、A6 为点的直角三角形有 12 个;如果 A1、A2、A3、……A2n 把圆周 2n 等分,则以 A1、A2、A3、…A2n为顶点的直角三角形有__________个,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展了“手机伴我健康行”主题活动.他们随机抽取部分学生进行“手机使用目的”和“每周使用手机时间”的问卷调查,并绘制成如图①②的统计图。已知“查资料”人人数是40人。
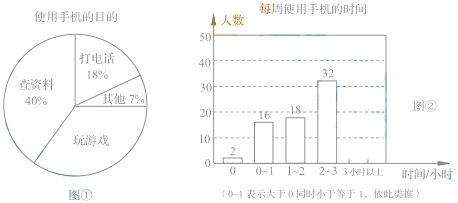
请你根据以上信息解答以下问题
(1)在扇形统计图中,“玩游戏”对应的圆心角度数是_______________。
(2)补全条形统计图
(3)该校共有学生1200人,估计每周使用手机时间在2小时以上(不含2小时)的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.某酒厂生产A,B两种品牌的酒,平均每天两种酒共可售出600瓶,每种酒每瓶的成本和售价如表所示,设平均每天共获利y元,平均每天售出A种品牌的酒x瓶.
A | B | |
成本(元) | 50 | 35 |
售价(元) | 70 | 50 |
(1)请写出y关于x的函数关系式;
(2)如果该厂每天至少投入成本25000元,且售出的B种品牌的酒不少于全天销售总量的55%,那么共有几种销售方案?并求出每天至少获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为 度.
(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用同样规格黑白两色的正方形瓷砖铺设长方形地面,请观察下列图形,并解答有关问题:
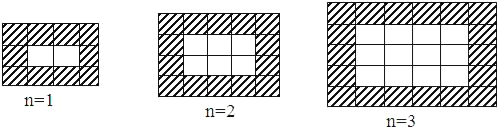
(1)在第n个图中,第一横行共 块瓷砖,第一竖列共有 块瓷砖;(均用含n的代数式表示)铺设地面所用瓷砖的总块数为 (用含n的代数式表示,n表示第n个图形)
(2)上述铺设方案,铺一块这样的长方形地面共用了506块瓷砖,求此时n的值;
(3)黑瓷砖每块4元,白瓷砖每块3元,在问题(2)中,共需要花多少钱购买瓷砖?
(4)是否存在黑瓷砖与白瓷砖块数相等的情形?请通过计算加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,等腰直角三角形OA1A2的直角边OA1在y轴的正半轴上,且OA1=A1A2=1,以OA2为直角边作第二个等腰直角三角形OA2A3,以OA3为直角边作第三个等腰直角三角形OA3A4,…,依此规律,得到等腰直角三角形OA2017A2018,则点A2017的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
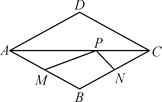
【题目】点P是菱形ABCD的对角线AC上的一个动点,已知AB=1,∠ADC=120°, 点M,N分别是AB,BC边上的中点,则△MPN的周长最小值是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com