
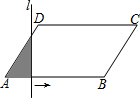
 如图,?ABCD中,AD=6,∠A=60°,AB=10,直线l⊥AB,且从点A开始向右匀速平行移动,每秒运动1个单位长度,设直线l扫过?ABCD的面积(阴影部分)为y,移动的时间为x秒,则当3≤x<10时,y与x的函数关系式是y=$\frac{3\sqrt{3}}{2}$x2-$\frac{9\sqrt{3}}{2}$x.
如图,?ABCD中,AD=6,∠A=60°,AB=10,直线l⊥AB,且从点A开始向右匀速平行移动,每秒运动1个单位长度,设直线l扫过?ABCD的面积(阴影部分)为y,移动的时间为x秒,则当3≤x<10时,y与x的函数关系式是y=$\frac{3\sqrt{3}}{2}$x2-$\frac{9\sqrt{3}}{2}$x. 分析 当3≤x<10时,如图所示直线l与AB、CD交于点E、F,作DM⊥AB于M,只要求出梯形DAEF的面积即可.
解答 解:当3≤x<10时,如图所示直线l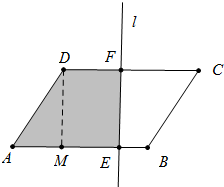 与AB、CD交于点E、F,作DM⊥AB于M.
与AB、CD交于点E、F,作DM⊥AB于M.
在RT△ADM中,∵∠AMD=90°,AD=6,∠A=60°,
∴AM=$\frac{1}{2}$AD=3,DM=$\sqrt{3}$AM=3$\sqrt{3}$,
∵l⊥AB,DM⊥AB,
∴AB∥CD,DM∥EF
∴四边形DMEF是平行四边形,
∵∠DME=90°,
∴四边形DMEF是矩形,
∴AE=x,DF=ME=x-3,
∴y=$\frac{1}{2}$(DF+AE)•DM=$\frac{1}{2}$•x(x-3)$•3\sqrt{3}$=$\frac{3\sqrt{3}}{2}$x2-$\frac{9\sqrt{3}}{2}$x.
故答案为y=$\frac{3\sqrt{3}}{2}$x2-$\frac{9\sqrt{3}}{2}$x.
点评 本题考查平行四边形的性质,进行的判断和性质、动点问题函数图象、30度直角三角形的性质等知识,解题的关键是正确画出图象,利用梯形面积公式解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
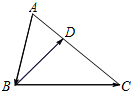 如图,在△ABC中,点D在AC边上且AD:DC=1:2,若$\overrightarrow{AB}=\overrightarrow{m}$,$\overrightarrow{BD}=\overrightarrow{n}$,那么$\overrightarrow{DC}$=2$\overrightarrow{m}$+2$\overrightarrow{n}$(用向量$\overrightarrow{m}$、$\overrightarrow{n}$表示).
如图,在△ABC中,点D在AC边上且AD:DC=1:2,若$\overrightarrow{AB}=\overrightarrow{m}$,$\overrightarrow{BD}=\overrightarrow{n}$,那么$\overrightarrow{DC}$=2$\overrightarrow{m}$+2$\overrightarrow{n}$(用向量$\overrightarrow{m}$、$\overrightarrow{n}$表示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=2}\\{y=1}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=-1}\\{z=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=-1}\\{z=-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2}\\{y=1}\\{z=1}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
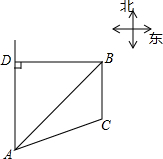 已知B港口位于A观测点的东北方向,且其到A观测点正北方向的距离BD的长为16千米,一艘货轮从B港口以48千米/时的速度沿如图所示的BC方向航行,15分后到达C处,现测得C处位于A观测点北偏东75°方向,求此时货轮与A观测点之间的距离AC的长(精确大0.1千米)
已知B港口位于A观测点的东北方向,且其到A观测点正北方向的距离BD的长为16千米,一艘货轮从B港口以48千米/时的速度沿如图所示的BC方向航行,15分后到达C处,现测得C处位于A观测点北偏东75°方向,求此时货轮与A观测点之间的距离AC的长(精确大0.1千米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
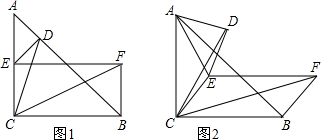
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
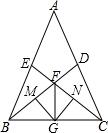 如图,在△ABC中,点E在AB上,点D在AC上,G为BC的中点,BE=CD,∠BEC=∠CDB,BD与CE相交于点F,GM⊥BF,GN⊥CF,垂足分别为M,N.
如图,在△ABC中,点E在AB上,点D在AC上,G为BC的中点,BE=CD,∠BEC=∠CDB,BD与CE相交于点F,GM⊥BF,GN⊥CF,垂足分别为M,N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com