

分析 (1)结论:BE+EF=2AH.如图②中,作AM⊥AE交EB的延长线于M.只要证明△DAE≌△BAM,利用△AEM是等腰直角三角形即可解决问题;
(2)结论:BE-EF=2AH.如图③中,在BH上取一点M,使得BM=EF.只要证明△ADE∽△ABM,推出∠EAD=∠MAB,推出∠EAM=∠DAB=90°,由HF=HM,EF=BM,可得EH=HM,即可推出EM=2AH,由此即可解决问题;
解答 解:(1)结论:BE+EF=2AH.
理由:如图②中,作AM⊥AE交EB的延长线于M.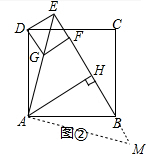
∵四边形ABCD、四边形DEFG都是正方形,
∴AD=AB,∠AEM=45°,∠DAB=∠EAM=90°,
∴∠DAE=∠BAM,∠M=∠AEM=45°,
∴AE=AM,
∵AH⊥EM,
∴EM=2AH,
在△DAE和△BAM中,
$\left\{\begin{array}{l}{AD=AB}\\{∠DAE=∠BAM}\\{AE=AM}\end{array}\right.$,
∴△DAE≌△BAM,
∴DE=EF=BM,
∴BE+EF=BE+BM=EM=2AH.
(2)结论:BE-EF=2AH.
理由:如图③中,在BH上取一点M,使得BM=EF.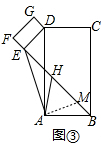
∵∠DEB=∠DAB=90°,易证∠EDA=∠ABM,
∵$\frac{AD}{AB}$=$\frac{DE}{EF}$=2,
∴$\frac{AD}{AB}$=$\frac{DE}{BM}$,
∴△ADE∽△ABM,
∴∠EAD=∠MAB,
∴∠EAM=∠DAB=90°,
∵HF=HM,EF=BM,
∴EH=HM,
∴EM=2AH,
∴BE-EF=BE-BM=EM=2AH,
∴BE-EF=2AH.
点评 本题考查四边形综合题、正方形的性质、全等三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形或相似三角形解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知一块圆心角为270°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60cm,则这块扇形铁皮的半径是40cm.
如图,已知一块圆心角为270°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60cm,则这块扇形铁皮的半径是40cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
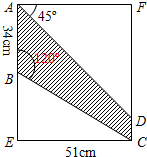 在2016首届合肥风筝文化节期间,某校丁周同学想在一个矩形材料中剪出如图阴影所示的图形,作为要制作的风筝的一个翅膀,请你根据图中的数据帮丁周同学计算出BE、CD的长度(精确到个位,$\sqrt{3}$≈1.7).
在2016首届合肥风筝文化节期间,某校丁周同学想在一个矩形材料中剪出如图阴影所示的图形,作为要制作的风筝的一个翅膀,请你根据图中的数据帮丁周同学计算出BE、CD的长度(精确到个位,$\sqrt{3}$≈1.7).查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 3 | B. | 4 | C. | 6 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com