



 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
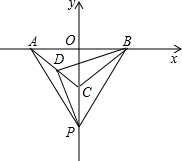
 如图,在平面直角坐标系中,直y=
如图,在平面直角坐标系中,直y=| 3 |
| 2 |
| 16 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
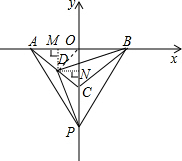
 如图,在平面直角坐标系中,原点O处有一乒乓球发射器向空中发射乒乓球,乒乓球飞行路线是一条抛物线,在地面上落点落在X轴上为点B.有人在线段OB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让乒乓球落入桶内.已知OB=4米,OC=3米,乒乓球飞行最大高度MN=5米,圆柱形桶的直径为0.5,高为0.3米(乒乓球的体积和圆柱形桶的厚度忽略不计).
如图,在平面直角坐标系中,原点O处有一乒乓球发射器向空中发射乒乓球,乒乓球飞行路线是一条抛物线,在地面上落点落在X轴上为点B.有人在线段OB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让乒乓球落入桶内.已知OB=4米,OC=3米,乒乓球飞行最大高度MN=5米,圆柱形桶的直径为0.5,高为0.3米(乒乓球的体积和圆柱形桶的厚度忽略不计).查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 3 |

查看答案和解析>>
科目:初中数学 来源:2012届重庆万州区岩口复兴学校九年级下第一次月考数学试卷(带解析) 题型:解答题
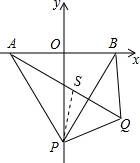
已知:直角梯形AOBC在平面直角坐标系中的位置如图,若AC∥OB,OC平分∠AOB,CB⊥x轴于B,点A坐标为(3 ,4). 点P从原点O开始以2个单位/秒速度沿x轴正向运动 ;同时,一条平行于x轴的直线从AC开始以1个单位/秒速度竖直向下运动 ,交OA于点D,交OC于点M,交BC于点E. 当点P到达点B时,直线也随即停止运动. 
(1)求出点C的坐标;
(2)在这一运动过程中, 四边形OPEM是什么四边形?请说明理由。若
用y表示四边形OPEM的面积 ,直接写出y关于t的函数关系式及t的
范围;并求出当四边形OPEM的面积y的最大值?
(3)在整个运动过程中,是否存在某个t值,使⊿MPB为等腰三角形?
若有,请求出所有满足要求的t值.
查看答案和解析>>
科目:初中数学 来源:2013年浙江省湖州市中考数学模拟试卷(十一)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com