
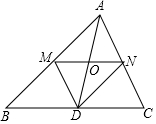
 如图,△ABC的中线AD与中位线MN相交于点O.AD与MN有怎样的关系?证明你的结论.
如图,△ABC的中线AD与中位线MN相交于点O.AD与MN有怎样的关系?证明你的结论.  名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AO、BO、CO、DO分别是四边形ABCD的四个内角的平分线.
如图,AO、BO、CO、DO分别是四边形ABCD的四个内角的平分线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如右图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移4格.
如右图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移4格.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AD∥BC,AB⊥BC于点B,AD=24cm,BC=26cm,点P从点A出发,以1cm/s的速度向点D运动,同时点Q从点C出发,以3cm/s的速度向点B运动,其中一个动点到达端点时另一个动点也随之停止运动,设运动时间为ts.
如图,在四边形ABCD中,AD∥BC,AB⊥BC于点B,AD=24cm,BC=26cm,点P从点A出发,以1cm/s的速度向点D运动,同时点Q从点C出发,以3cm/s的速度向点B运动,其中一个动点到达端点时另一个动点也随之停止运动,设运动时间为ts.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABC是定圆O的内接三角形,AD为△ABC的高线,AE平分∠BAC交⊙O于E,交BC于G,连OE交BC于F,连OA,在下列结论中,①CE=2EF,②△ABG∽△AEC,③∠BAO=∠DAC,④$\frac{AB•AC}{AD}$为常量.其中正确的有②,③,④.
如图,△ABC是定圆O的内接三角形,AD为△ABC的高线,AE平分∠BAC交⊙O于E,交BC于G,连OE交BC于F,连OA,在下列结论中,①CE=2EF,②△ABG∽△AEC,③∠BAO=∠DAC,④$\frac{AB•AC}{AD}$为常量.其中正确的有②,③,④.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com