
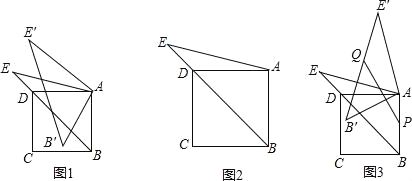
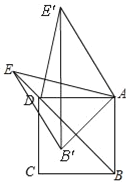
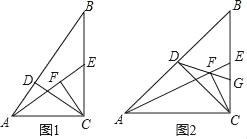
����Ŀ����֪��������ABCD�ı߳�Ϊ4����E�ǶԽ���BD�ӳ�����һ�㣬AE=BD������ABE�Ƶ�A˳ʱ����ת���ȣ�0�㣼����360�㣩�õ���AB��E�䣬��B��E�Ķ�Ӧ��ֱ�ΪB�䡢E�䣮
��1����ͼ1������=30��ʱ����֤��B��C=DE��
��2������B��E��DE�䣬��B��E=DE��ʱ������ͼ2�����ֵ��
��3����ͼ3����PΪAB���е㣬��QΪ�߶�B��E��������һ�㣬��̽�����ڴ���ת�����У��߶�PQ���ȵ�ȡֵ��ΧΪ�� ����
���𰸡���1��֤����������2��45�㣨3��![]() ��PQ��4
��PQ��4![]() +2
+2
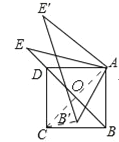
�����������������(1)������AC��B��C�����������ε����ʵó��ó�AC=AE=2OA������Rt��AOE�����ʵó���E=30�㣬Ȼ������תͼ�ε����ʵó���ADE�͡�AB��Cȫ�ȣ��Ӷ��ó��𰸣�(2)��������תͼ�ε����ʵó���AEB��͡�AE��Dȫ�ȣ��Ӷ��ó���DAE��=��EAB�䣬Ȼ������תͼ�ε����ʵó���EAE��=��BAB�䣬�Ӷ��õ���BAB��=��DAB�䣬�����ݡ�BAB��+��DAB��=90��ó��𰸣�(3)����P��PM��BE����AB=4����P��AB�е㣬����BP=2�ó�PM=![]() ������ת�����У���ABE����ת����E��BA���ӳ���ʱ����Q�͵�E�غϣ�Ȼ�����PQ�ij��ȣ��Ӷ��ó�ȡֵ��Χ.
������ת�����У���ABE����ת����E��BA���ӳ���ʱ����Q�͵�E�غϣ�Ȼ�����PQ�ij��ȣ��Ӷ��ó�ȡֵ��Χ.
�����������1����ͼ������AC��B��C�� ���ı���ABCD�������Σ�
��AB=AD��AC��BD��AC=BD=2OA����CAB=ADB=45�㣬 ��AE=BD�� ��AC=AE=2OA��
��Rt��AOE�У���AOE=90�㣬AE=2OA�� ���E=30�㣬
���DAE=��ADB����E=45�㩁30��=15�㣬 ����ת�У�AD=AB=AB���BAB��=30��
���DAE=15�㣬
�ڡ�ADE�͡�AB��C�У� 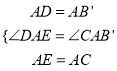 �� ���ADE�ա�AB��C����DE=B��C��
�� ���ADE�ա�AB��C����DE=B��C��
��2����ͼ��
����ת�ã�AB��=AB=AD��AE��=AE��
�ڡ�AEB��͡�AE��D�У� 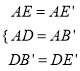 �����AEB��ա�AE��D�����DAE��=��EAB�䣬
�����AEB��ա�AE��D�����DAE��=��EAB�䣬
���EAE��=��DAB�䣬����ת�ã���EAE��=��BAB�䣬���BAB��=��DAB�䣬
�ߡ�BAB��+��DAB��=90�㣬���=��BAB��=45�㣬
��3����ͼ���ɵ㵽ֱ�ߵľ��룬����P��PM��BE����AB=4����P��AB�е㣬
��BP=2����PM=![]() ��
��
����ת�����У���ABE����ת����E��BA���ӳ���ʱ����Q�͵�E�غϣ�
��AQ=AE=BQ=4![]() ��PQ=AQ+AP=4
��PQ=AQ+AP=4![]() +2��
+2��
�ʴ�Ϊ![]() ��PQ��4
��PQ��4![]() +2��
+2��



 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
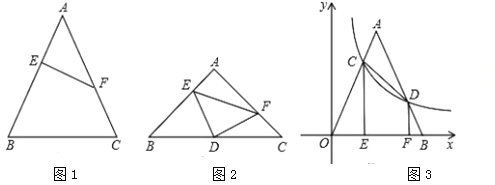
����Ŀ����ͼ1������![]() �У���
�У���![]() �ֱ�����
�ֱ�����![]() �ϣ�����
�ϣ�����![]() ����
����![]() �����
�����![]() Ϊ�õ��������ε�����ߣ�
Ϊ�õ��������ε�����ߣ�
��1����ͼ1��![]() �ǵ���
�ǵ���![]() ������ߣ���
������ߣ���![]() ���������
���������![]() �ij���
�ij���
��2����ͼ2����ֱ��![]() ��ֱ�Ƕ���
��ֱ�Ƕ���![]() ǡ��Ϊ����ֱ��
ǡ��Ϊ����ֱ��![]() �ױ�
�ױ�![]() �ϵ��е㣬�ҵ�
�ϵ��е㣬�ҵ�![]() �ֱ���
�ֱ���![]() �ϣ���֤��
�ϣ���֤��![]() Ϊ����
Ϊ����![]() ������ߣ�
������ߣ�
��3����ͼ3������![]() �Ķ���
�Ķ���![]() ��ԭ���غϣ��ױ�
��ԭ���غϣ��ױ�![]() ��
��![]() ���ϣ�����������
���ϣ�����������![]() ��ͼ��
��ͼ��![]() �ڵ�
�ڵ�![]() ����
����![]() ǡΪ
ǡΪ![]() ������ߣ�����
������ߣ�����![]() �ֱ���
�ֱ���![]() ���ڵ�
���ڵ�![]() ���ڵ�
���ڵ�![]() ����֪
����֪![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
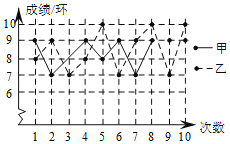
����Ŀ����ͼ�Ǽס���������˶�Ա10������ɼ�������ͳ��ͼ����ô����ͼ�е���Ϣ���ƣ�����10�������Ը������__��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
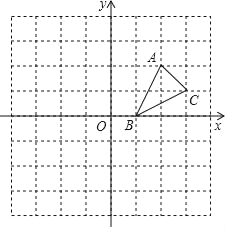
����Ŀ����ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ��ڽ���ƽ��ֱ������ϵ����ABC�Ķ�����ڸ���ϣ���B������Ϊ��1��0����
��1��������ABC����x��ԳƵ���A1B1C1��
��2����������ABC��ԭ��O����ʱ����ת90�����õ���A2B2C2����д����C2�����ꣻ
��3����A1B1C1����A2B2C2�����ĶԳ����������ĶԳƣ�д���Գ����ĵ����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�ֶ�������n����F���������ٵ�nΪ����ʱ�����Ϊ3n+5���ڵ�nΪż��ʱ�����Ϊ![]() ������k��ʹ
������k��ʹ![]() Ϊ��������С�������������������ظ����У����磺ȡn��26�������������ͼ��
Ϊ��������С�������������������ظ����У����磺ȡn��26�������������ͼ��
![]()
��ô��n��9ʱ����2019����F�������Ľ����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˽ⱾУ���꼶ѧ������ѵ���������������꼶������ѧ�����в��ԣ�Ȼ��Ѳ��Խ����Ϊ4���ȼ���A��B��C��D������ͳ�ƽ�����Ƴ�������������ͳ��ͼ�������ͼ�е���Ϣ����������⣺

��1������ε����У�һ�������� ��ѧ��������ͳ��ͼ�У�C�ȼ���Ӧ������Բ�Ľ��� �� ����.
��2����ȫ����ͳ��ͼ.
��3�����꼶����900�ˣ����Ƹ��꼶������Գɼ�ΪD�ȵ�����Ϊ�� ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����е�����ճ������г�����һ���ӱ�������ӱ���ͬ����е���ܻ�������о�����ص�Ӱ�쳣�������ʱ����Ϊ�˱Ƚ��г��ϼס��������е���ľ��ȣ���������У��������ȡһ�����ÿ����ʱ���ļ�⣬�������10�죬�����ÿ����ʱ����ͳ��������ͼ(��λ����)��
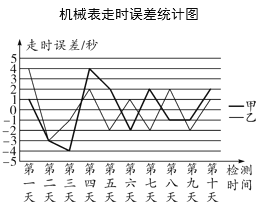
��1���ס������ֻ�е����ƽ����ʱ���ֱ��Ƕ��٣�
��2��С���ּƻ�����һ���е�������������ʱ��ȷ�ȿ��ǣ�����Ƽ�������ס�����һ�֣���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
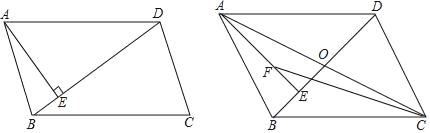
����Ŀ����֪����ͼ1����ABC�У���ACB=90�㣬CD��AB��D��EΪBC�е㣬CF��AE��F��
��1����֤��4CE2=BDAB��
��2����2��DCF=��ECF����cos��ECF��ֵ��
��3����ͼ2��DF�ӳ��߽�BC��G����AC=BC��EG=1����DG=�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�AE��BD��E��
��1����BC��BD��![]() ��AD��15�����ABD���ܳ���
��AD��15�����ABD���ܳ���
��2������DBC��45�㣬�Խ���AC��BD���ڵ�O��FΪAE��һ�㣬��AF��2EO����֤��CF��![]() AB��
AB��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com