
 处,折痕为EF,若∠ABE=20°,那么
处,折痕为EF,若∠ABE=20°,那么 的度数为 。
的度数为 。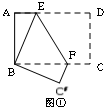
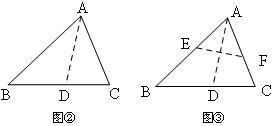
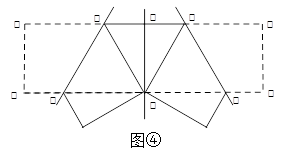
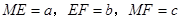 ,根据折叠的性质及勾股定理可证得△MPF为等边三角形,则∠MFE=30°,∠MFN=60°,又MN=MF=
,根据折叠的性质及勾股定理可证得△MPF为等边三角形,则∠MFE=30°,∠MFN=60°,又MN=MF=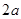 ,则△MNF为等边三角形,即可求得结果;
,则△MNF为等边三角形,即可求得结果; =∠EFC=125°;
=∠EFC=125°;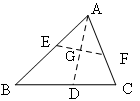
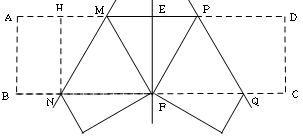
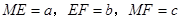
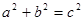 ①
① 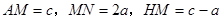
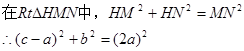 ②
② 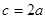


科目:初中数学 来源:不详 题型:单选题
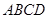 的场地,长
的场地,长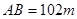 ,宽
,宽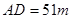 ,从
,从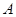 、
、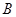 两处入口的中路宽都为
两处入口的中路宽都为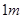 ,两小路汇合处路宽为
,两小路汇合处路宽为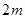 ,其余部分种植草坪,则草坪面积为( )
,其余部分种植草坪,则草坪面积为( )
A.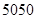 m2 m2 | B.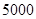 m2 m2 | C.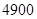 m2 m2 | D. m2 m2 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
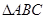 的顶点坐标分别为A(-4,-3) B(0,-3) C(-2,1),如将B点向右平移2个单位再向上平移4个单位到达B1点,若设
的顶点坐标分别为A(-4,-3) B(0,-3) C(-2,1),如将B点向右平移2个单位再向上平移4个单位到达B1点,若设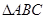 的面积为
的面积为 ,
,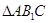 的面积为
的面积为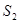 ,则
,则 ,
,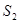 的大小关系为( )
的大小关系为( )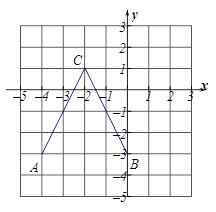
A. > >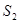 | B. = =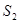 | C. < <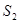 | D.不能确定 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com