Question

19．已知△ACB为等腰直角三角形，∠ACB=90°，点E在AC上，EF⊥AC交AB于F，连BE、CF，M、N分别为CF、BE的中点．
（1）如图1，则$\frac{MN}{CE}$=$\frac{1}{2}$，并说明理由；
（2）如图2，将△AEF绕点A顺时针旋转45°，（1）中的结论是否成立？并加以证明；
（3）如图3，将△AEF绕A点顺时针旋转一个锐角，则上述结论是否仍成立？（画图不证明）

Answer 1

分析 （1）首先证明△CMG≌△FME，由全等三角形的性质可得：MG=ME，CG=EF，所以MN $\frac{1}{2}$=BG=$\frac{1}{2}$（BC-CG）=$\frac{1}{2}$（AC-AE）=$\frac{1}{2}$CE，即 $\frac{MN}{CE}$=$\frac{1}{2}$，
（2）将△AEF绕点A顺时针旋转45°，（1）中的结论仍旧成立，取CE中点G，连结MG、NG，通过证明△MNG∽△ECA，即可得到问题答案；
（3）将△AEF绕A点顺时针旋转一个锐角，（1）中的结论仍旧成立，取CE中点G，连结MG、NG，先判断出∠MGN=∠CAE，$\frac{MG}{AE}$=$\frac{NG}{AC}$=$\frac{1}{2}$，得出△MNG∽△ECA，即可得到问题答案．

解答 解：（1）如图1，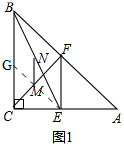

延长EM，交BC于G，
∵FE⊥AC，∠ACB=90°，
∴EF∥BC，
∴∠MCG=∠MFE，∠MGC=∠MEF，
又∵CM=FM，
∴△CMG≌△FME，
∴MG=ME，CG=EF，
又∵BN=EN，
∴NM=$\frac{1}{2}$BG，
∵∠EFA=∠A=45°，
∴AE=EF=CG，
又∵BC=AB，
∴MN $\frac{1}{2}$=BG=$\frac{1}{2}$（BC-CG）=$\frac{1}{2}$（AC-AE）=$\frac{1}{2}$CE，
即 $\frac{MN}{CE}$=$\frac{1}{2}$，
故答案为 $\frac{1}{2}$；

（2）将△AEF绕点A顺时针旋转45゜，（1）中的结论仍旧成立，
理由如下：
如图2，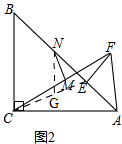

取CE中点G，连结MG、NG，
则MG=$\frac{1}{2}$EF=$\frac{1}{2}$AE，NG=$\frac{1}{2}$BC=$\frac{1}{2}$AC，
∵EF与BC所成角为45°，MG∥EF，
∴MG与BC所成角为45°，
又∵NG∥BC，
∴∠NGM=45°=∠BAC，
又∵$\frac{MG}{AE}$=$\frac{NG}{AC}$=$\frac{1}{2}$，
∴△MNG∽△ECA，
∴$\frac{MN}{CE}$=$\frac{1}{2}$．
（3）将△AEF绕A点顺时针旋转一个锐角，（1）中的结论仍旧成立，
理由如下：
如图3，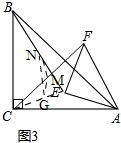

取CE中点G，连结MG、NG，
则MG=$\frac{1}{2}$EF=$\frac{1}{2}$AE，NG=$\frac{1}{2}$BC=$\frac{1}{2}$AC，
NG∥BC，MG∥EF，
∴∠NGE=∠BCE，∠MGE+∠CEF=180°，
∴∠MGN=∠EGN-∠EGM=∠BCE-（180°-∠CEF）=90°-∠ACE-[180°-（360°-90°-∠AEC）]=180°-∠ACE-∠AEC=∠CAE，
又∵$\frac{MG}{AE}$=$\frac{NG}{AC}$=$\frac{1}{2}$，
∴△MNG∽△ECA，
∴$\frac{MN}{CE}$=$\frac{1}{2}$．

点评 此题是几何变换综合题，主要考查了全等三角形的判定和性质、三角形的中位线定理、图形的旋转的性质以及相似三角形的判定和性质，直角三角形的性质，解本题的关键是判断出∠MGN=∠CAE，题目的综合性很强，难度不小．