

分析 (1)如图1中,连接EO,延长EO交CD于F,连接DO,设半径为x.构建方程即可解决问题.
(2)如图2中,作OP⊥BC于P,连接ON,则OD=ON=5,在Rt△OPN中,求出PN2即可解决问题.
解答 解:(1)连接EO,延长EO交CD于F,连接DO,设半径为x.
∵AB切○O于E,
∴EF⊥AB,
∵AB∥CD,
∴EF⊥CD,
∴∠OFD=90°,
在Rt△DOF中,∵∠OFD=90°,OF2+DF2=OD2,
∴x2=(8-x)2+42,
∴x=5,
∴⊙O的半径为5.
(2)如图2中,作OP⊥BC于P,连接ON,则OD=ON=5,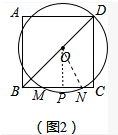
∵四边形ABCD是正方形,
∴BD=8$\sqrt{2}$,OB=BD-OD=8$\sqrt{2}$-5,OP=$\frac{8\sqrt{2}-5}{\sqrt{2}}$=8-$\frac{5\sqrt{2}}{2}$,
∴PN2=ON2-OP2=52-(8-$\frac{5\sqrt{2}}{2}$)2=40$\sqrt{2}$-51.5,
∵MN=2PN,
∴MN2=4PN2=4(40$\sqrt{2}$-51.5)=160$\sqrt{2}$-206.
点评 本题考查切线的性质、正方形的性质、垂径定理、勾股定理等知识,解题的关键是灵活运用这些知识解决问题,学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
 已知:二次函数y1=x2+bx+c的图象经过A(-1,0),B(0,-3)两点.
已知:二次函数y1=x2+bx+c的图象经过A(-1,0),B(0,-3)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,点A(-2,1),B(-3,0),C(-1,1).请在平面直角坐标系xOy中分别标出点A,B,C的位置,顺次连接A、B、C三点,并将三角形ABC向右平移3个单位,向下平移1个单位,画出平移后的图形.
已知,点A(-2,1),B(-3,0),C(-1,1).请在平面直角坐标系xOy中分别标出点A,B,C的位置,顺次连接A、B、C三点,并将三角形ABC向右平移3个单位,向下平移1个单位,画出平移后的图形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两边及其一边的对角对应相等的两个三角形全等 | |
| B. | “明天的降水概率是80%”表示明天会有80%的地方下雨 | |
| C. | 一个不透明的袋中装有8个红球和1个黄球,从中摸出一个球是红球是随机事件 | |
| D. | 打开电视机,它“正在播广告”是必然事件 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点p(-1,0),以O1,O2,O3,…为圆心在x轴正半轴上连续作圆,半径分别为1,2,3,…,过点P作各圆的切线,切点分别为A1、A2、A3,…,则sin∠AnPOn=$\frac{n}{{n}^{2}+1}$.
如图,点p(-1,0),以O1,O2,O3,…为圆心在x轴正半轴上连续作圆,半径分别为1,2,3,…,过点P作各圆的切线,切点分别为A1、A2、A3,…,则sin∠AnPOn=$\frac{n}{{n}^{2}+1}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com