
【题目】如图,E,F,G,H分别是边AB,BC,CD,DA的中点. 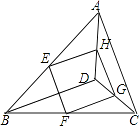
(1)判断四边形EFGH的形状,并证明你的结论;
(2)当BD,AC满足什么条件时,四边形EFGH是正方形.(不要求证明)
【答案】
(1)解:在△ABC中,E、F分别是边AB、BC中点,
所以EF∥AC,且EF= ![]() AC,
AC,
同理有GH∥AC,且GH= ![]() AC,
AC,
∴EF∥GH且EF=GH,
故四边形EFGH是平行四边形.
(2)解:EH∥BD且EH= ![]() BD,
BD,
若AC=BD,则有EH=EF,
又因为四边形EFGH是平行四边形,
∴四边形EFGH是菱形,
∵AC⊥BD,
∴∠EHG=90°,
即:当AC=BD且AC⊥BD时,四边形EFGH是正方形.
【解析】(1)在△ABC中,E、F分别是边AB、BC中点,得到EF∥AC,且EF= ![]() AC,GH∥AC,且GH=
AC,GH∥AC,且GH= ![]() AC,得到四边形EFGH是平行四边形;(2)四边形EFGH是平行四边形,再由AC=BD,得出EH=EF,从而证得四边形EFGH是菱形.对角线相等,推知四边形EFGH是正方形;
AC,得到四边形EFGH是平行四边形;(2)四边形EFGH是平行四边形,再由AC=BD,得出EH=EF,从而证得四边形EFGH是菱形.对角线相等,推知四边形EFGH是正方形;


科目:初中数学 来源: 题型:
【题目】一个四边形的三个内角的度数依次如下,那么其中是平行四边形的是( )
A. 88°,108°,88° B. 88°,104°,88°
C. 88°,92°,92° D. 88°,92°,88°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是一个菱形绿地,其周长为40 ![]() m,∠ABC=120°,在其内部有一个四边形花坛EFGH,其四个顶点恰好在菱形ABCD各边的中点,现在准备在花坛中种植茉莉花,其单价为10元/m2 , 请问需投资金多少元?(结果保留整数)
m,∠ABC=120°,在其内部有一个四边形花坛EFGH,其四个顶点恰好在菱形ABCD各边的中点,现在准备在花坛中种植茉莉花,其单价为10元/m2 , 请问需投资金多少元?(结果保留整数) 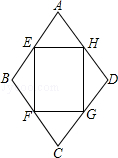
查看答案和解析>>
科目:初中数学 来源: 题型:
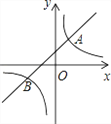
【题目】如图,已知一次函数![]() (
(![]() 为常数,且
为常数,且![]() )的图象与反比例函数
)的图象与反比例函数![]() (
(![]() 为常数,且
为常数,且![]() )的图象相交于
)的图象相交于![]() 两点.
两点.
(1)求一次函数和反比例函数的解析式;
(2)若![]() 为反比例函数图象上的三点,且
为反比例函数图象上的三点,且![]() 请直接写出
请直接写出![]() 的大小关系式;
的大小关系式;
(3)结合图象,请直接写出关于![]() 的不等式
的不等式![]() >
>![]() 的解集.
的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com