
 。
。 的长。
的长。 
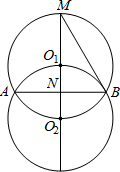
解:如图,连结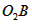 , ,∵⊙O1和⊙O2是等圆,且O1在⊙O2上, ∴点O2也在⊙O1上, ∵O1O2是两圆的连心线, ∴MO2是⊙O1的直径, ∴∠MBO2=90°, 又∵直线BM经过半径的O2B的外端, ∴直线BM是⊙O2的切线; |
 |
| (2)连结O1A、O1B, ∵点B既在⊙O1上,又在⊙O2上, ∴O1O2=O1B=O2B, ∴∠NO1B=60°, ∵O1O2是两圆的连心线, ∴O1O2⊥AB,BN= 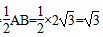 , ,在Rt△NO1B中,sin60°= 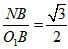 ,O1B=2, ,O1B=2,∵O1M=O1B, ∴∠O1MB =∠O1BM= 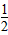 ∠BO1N = ∠BO1N =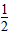 ×60°=30°, ×60°=30°,∴在Rt△MBN中,∠MBN= 60°, ∴∠MO1A=120°, ∴ 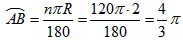 。 。 |


科目:初中数学 来源: 题型:
 于点N,连接BM,已知AB=2
于点N,连接BM,已知AB=2| 3 |
 |
| AM |
查看答案和解析>>
科目:初中数学 来源: 题型:
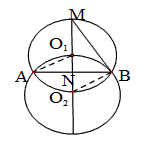
 (2012•桂林)如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心,顺次连接A、O1、B、O2.
(2012•桂林)如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心,顺次连接A、O1、B、O2.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•梧州模拟)如图:等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心,顺次连接A、O1、B、O2.
(2013•梧州模拟)如图:等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心,顺次连接A、O1、B、O2.查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(广西桂林卷)数学(带解析) 题型:解答题
如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心,顺次连接
A、O1、B、O2.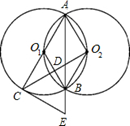
(1)求证:四边形AO1BO2是菱形;
(2)过直径AC的端点C作⊙O1的切线CE交AB的延长线于E,连接CO2交AE于D,求证:CE=2O2D;
(3)在(2)的条件下,若△AO2D的面积为1,求△BO2D的面积.
查看答案和解析>>
科目:初中数学 来源:2013届广西桂林市初中毕业升学模拟考试数学试卷(带解析) 题型:解答题
如图:等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心,顺次连接A、O1、B、O2.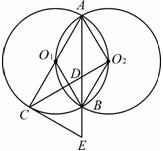
(1)求证:四边形AO1BO2是菱形;
(2)过直径AC的端点C作⊙O1的切线CE交AB的延长线于E,连接CO2交AE于D,求证:CE=2DO2;
(3)在(2)的条件下,若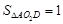 ,求
,求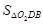 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com