练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．运用完全平方公式计算
    ①2012
    ②99.82
    ③（3α-4b）2-（3α+4b）2 
    ④（2x-3y）2-（4y-3x）（4y+3x）

    分析 ①先将原式变形为（200+1）2，再根据完全平方公式展开即可；
    ②先将原式变形为（10-0.2）2，再根据完全平方公式展开即可；
    ③根据完全平方公式展开，再合并同类项即可；
    ④根据完全平方公式和平方差公式展开，再合并同类项即可．

    解答 解：①原式=（200+1）2
    =40000+400+1
    =40401．
                                       
    ②原式=（10-0.2）2
    =100-4+0.04
    =95.96．

    ③（3a-4b）2-（3a+4b）2
    =9a2-24ab+16b2-9a2-24ab-16b2
    =-48ab．

    ④（2x-3y）2-（4y-3x）（4y+3x）
    =4x2-12xy+9y2-16y2+9x2
    =13x2-12xy-7y2．

    点评 本题考查了平方差公式和完全平方公式的应用，主要考查学生的计算能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    1．已知抛物线y=x2-2bx+$\frac{1}{4}$的顶点在x轴上，则b的值是$±\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．当y=10时，代数式3y-1比4y-6的值小5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．下列方程组中，是三元一次方程组的是（　　）
    A．$\left\{\begin{array}{l}{a=1}\\{b=2}\\{b-c=3}\\{\;}\end{array}\right.$B．$\left\{\begin{array}{l}{x+y=2}\\{y+z=1}\\{z+c=3}\\{\;}\end{array}\right.$
    C．$\left\{\begin{array}{l}{4x-3y=7}\\{5x-2y=14}\\{2x-y=4}\\{\;}\end{array}\right.$D．$\left\{\begin{array}{l}{xy+z=3}\\{x+yz=5}\\{xy+y=7}\\{\;}\end{array}\right.$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．分解因式：（m+n）（m2-mn+n2）-n2（m+n）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．设抛物线y=a（x-m）2+n（m≠0）与y轴交于点A，顶点为B，点A、B关于原点的对称点分别为C、D．称直线AB为抛物线的伴随直线，四边形ABCD为抛物线的伴随四边形．
    （1）求抛物线y=（x-2）2+1的伴随直线的解析式，伴随四边形的顶点坐标．
    （2）若抛物线y=a（x-m）2+n（m≠0）的伴随直线是y=-2x+5，试解决下列问题：
    ①若伴随四边形的面积为5，求此抛物线顶点坐标；
    ②若伴随四边形ABCD是矩形，在抛物线的对称轴上是否存在点P，使得△PBD是一个以PD为底边的等腰三角形？若存在，请写出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

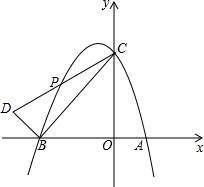    8．如图，抛物线y=-$\frac{1}{2}$x2+bx+4与x轴交于A（2，0）、B两点，与y轴交于点C．
    （1）求b的值；
    （2）求抛物线的对称轴及顶点坐标；
    （3）以点B为直角顶点，BC为直角边作Rt△BCD，CD交抛物线于第二象限的点P，若PC=PD，求P点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

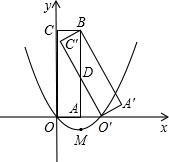    5．如图，矩形A′BC′O′是矩形OABC（边OA在x轴正半轴上，边OC在y轴正半轴上）绕B点逆时针旋转得到的，O′点在x轴的正半轴上，B点的坐标为（1，3）．
    （1）直接写出OA与O′A的数量关系；
    （2）如果二次函数y=ax2+bx+c（a≠0）的图象经过O、O′两点且图象顶点M的纵坐标为-1：
    ①在二次函数对称轴右侧的图象是否存在点P，使得△POM为直角三角形？若存在，请求出P点的坐标和四边形POMO′的面积；若不存在，请说明理由；
    ②若C′O′与AB相交于点D，在对称轴上是否存在一点Q，使得∠A′QD=∠BA′D？若存在，求出点Q坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．设边长为a的正方形的面积为2．下列关于a的三种说法：①a是无理数；②a可以用数轴上的一个点来表示；
    ③1＜a＜2．其中，所有正确的序号是（　　）
    A．①②B．①③C．②③D．①②③

    查看答案和解析>>

    同步练习册答案