
分析 根据把平面内与四边形各边端点构成的三角形都是等腰三角形的点叫做这个四边形的腰点,可得正方形一共有9个腰点,除了正方形的中心外,两条与边平行的对称轴上各有四点,据此解答即可.
解答 解:如图,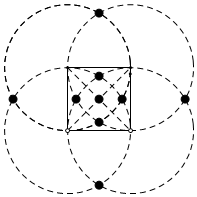
正方形一共有9个腰点,除了正方形的中心外,两条与边平行的对称轴上各有四个腰点.
故答案为:9.
点评 (1)此题主要考查了正方形的性质和应用,要熟练掌握,解答此题的关键是要明确:①正方形的四条边都相等,四个角都是直角;②正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;③正方形具有四边形、平行四边形、矩形、菱形的一切性质.④两条对角线将正方形分成四个全等的等腰直角三角形,同时,正方形又是轴对称图形,有四条对称轴.
(2)此题还考查了等腰三角形的性质和应用,考查了分类讨论思想的应用,要熟练掌握,解答此题的关键是要明确:①等腰三角形的两腰相等.②等腰三角形的两个底角相等.③等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.


科目:初中数学 来源: 题型:选择题
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x | … | -3 | -2 | -1 | 0 | … |
| y | … | -2 | -5 | -6 | -5 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
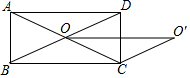 如图,矩形ABCD的对角线AC、BD交于点O,∠AOB=40°.
如图,矩形ABCD的对角线AC、BD交于点O,∠AOB=40°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
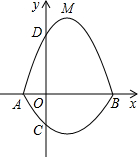 如图所示,在平面直角坐标系中,A、B为x轴上两点,C、D为y轴上两点,经过点A,C,B的抛物线的一部分C1与经过点A,D,B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.
如图所示,在平面直角坐标系中,A、B为x轴上两点,C、D为y轴上两点,经过点A,C,B的抛物线的一部分C1与经过点A,D,B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com