
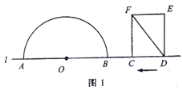
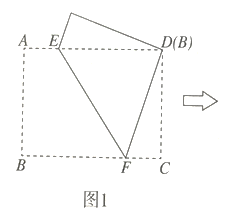
【题目】如图1,点![]() 和矩形
和矩形![]() 的边
的边![]() 都在直线
都在直线![]() 上,以点
上,以点![]() 为圆心,以24为半径作半圆,分别交直线
为圆心,以24为半径作半圆,分别交直线![]() 于
于![]() 两点.已知:
两点.已知: ![]() ,
,![]() ,矩形自右向左在直线
,矩形自右向左在直线![]() 上平移,当点
上平移,当点![]() 到达点
到达点![]() 时,矩形停止运动.在平移过程中,设矩形对角线
时,矩形停止运动.在平移过程中,设矩形对角线![]() 与半圆
与半圆![]() 的交点为
的交点为![]() (点
(点![]() 为半圆上远离点
为半圆上远离点![]() 的交点).
的交点).
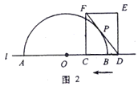
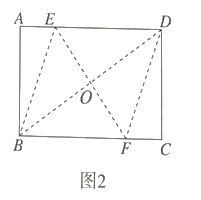
(1)如图2,若![]() 与半圆
与半圆![]() 相切,求
相切,求![]() 的值;
的值;
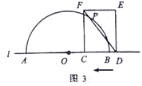
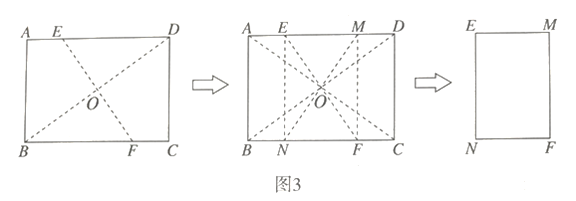
(2)如图3,当![]() 与半圆
与半圆![]() 有两个交点时,求线段
有两个交点时,求线段![]() 的取值范围;
的取值范围;
(3)若线段![]() 的长为20,直接写出此时
的长为20,直接写出此时![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)如图2,连接OP,则DF与半圆相切,利用△OPD≌△FCD(AAS),可得:OD=DF=30;
(2)利用![]() ,求出
,求出![]() ,则
,则![]() ;DF与半圆相切,由(1)知:PD=CD=18,即可求解;
;DF与半圆相切,由(1)知:PD=CD=18,即可求解;
(3)设PG=GH=m,则:![]()
![]()
![]() ,求出
,求出![]() ,利用
,利用![]() ,即可求解.
,即可求解.
(1)如图,连接![]()
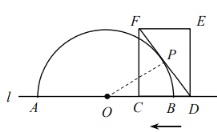
∵![]() 与半圆相切,∴
与半圆相切,∴![]() ,∴
,∴![]() ,
,
在矩形![]() 中,
中,![]() ,
,
∵![]() ,根据勾股定理,得
,根据勾股定理,得
![]()
在![]() 和
和![]() 中,
中,
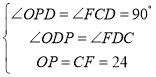
∴![]()
∴![]()
(2)如图,
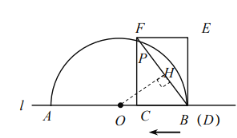
当点![]() 与点
与点![]() 重合时,
重合时,
过点![]() 作
作![]() 与点
与点![]() ,则
,则![]()
∵![]()
且![]() ,由(1)知:
,由(1)知:![]()
∴![]() ,∴
,∴![]() ,
,
∴![]()
当![]() 与半圆相切时,由(1)知:
与半圆相切时,由(1)知:![]() ,
,
∴![]()
(3)设半圆与矩形对角线交于点P、H,过点O作OG⊥DF,
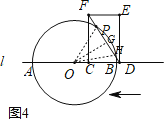
则PG=GH,
![]() ,则
,则![]() ,
,
设:PG=GH=m,则:![]() ,
,
![]() ,
,
整理得:25m2-640m+1216=0,
解得:![]() ,
,
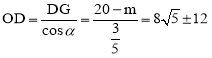 .
.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】综合与实践
![]() 纸是我们学习工作最常用的纸张之一, 其长宽之比是
纸是我们学习工作最常用的纸张之一, 其长宽之比是![]() ,我们定义:长宽之比是
,我们定义:长宽之比是![]() 的矩形纸片称为“标准纸”.
的矩形纸片称为“标准纸”.
操作判断:
![]() 如图1所示,矩形纸片
如图1所示,矩形纸片![]() 是一张“标准纸”,将纸片折叠一次,使点
是一张“标准纸”,将纸片折叠一次,使点![]() 与
与![]() 重合,再展开,折痕
重合,再展开,折痕![]() 交
交![]() 边于点
边于点![]() 交
交![]() 边于点
边于点![]() ,若
,若![]() 求
求![]() 的长,
的长,
![]() 如图2,在
如图2,在![]() 的基础上,连接
的基础上,连接![]() 折痕
折痕![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 判断四边形
判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
探究发现:
![]() 如图3所示,在(1)和(2)的基础上,展开纸片后,将纸片再折叠一次,使点
如图3所示,在(1)和(2)的基础上,展开纸片后,将纸片再折叠一次,使点![]() 与点
与点![]() 重合,再展开,痕
重合,再展开,痕![]() 交
交![]() 边于点
边于点![]() ,
,![]() 交边于点
交边于点![]() 交
交![]() 也是点
也是点![]() .然后将四边形
.然后将四边形![]() 剪下,探究纸片
剪下,探究纸片![]() 是否为“标准纸”,说明理由.
是否为“标准纸”,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,点
,点![]() 在抛物线上,且
在抛物线上,且![]() .
.![]() 与
与![]() 轴相交于点
轴相交于点![]() ,过点
,过点![]() 的直线
的直线![]() 平行于
平行于![]() 轴,与抛物线相交于
轴,与抛物线相交于![]() ,
,![]() 两点,则线段
两点,则线段![]() 的长为( )
的长为( )
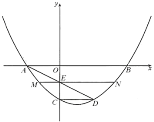
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=2![]() ,点P为AB边上的一个动点,连接PC,过点P作PQ⊥PC交BC边于点Q,则BQ的最大值为_____.
,点P为AB边上的一个动点,连接PC,过点P作PQ⊥PC交BC边于点Q,则BQ的最大值为_____.
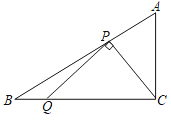
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展征文活动,征文主题只能从“爱国”、“敬业”、“诚信”、“友善”四个主题中选择一个,每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.

(1)将上面的条形统计图补充完整;
(2)在扇形统计图中,选择“爱国”主题所对应的圆心角是_____度;
(3)如果该校七年级共有1200名考生,请估计选择以“友善”为主题的七年级学生有______名;
(4)学生会宣传部有七年级的2名男生和2名女生,现从中随机挑选2名同学参加“主题征文”宣传活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学兴趣小组的同学们对函数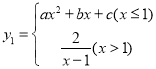 的图象和性质进行了探究,已知
的图象和性质进行了探究,已知![]() 时,函数
时,函数![]() 的图象的对称轴为直线
的图象的对称轴为直线![]() ,顶点在
,顶点在![]() 轴上,与
轴上,与![]() 轴的交点坐标为
轴的交点坐标为![]() ,探究过程如下,请补充过程:
,探究过程如下,请补充过程:
(1)![]() ,
,![]() ,
,![]() .
.
(2)在给出的平面直角坐标系中,画出函数图象,并写出这个函数的一条性质: .
(3)进一步探究函数图象并解决问题:
①若![]() 有三个实数解,则
有三个实数解,则![]() 的取值范围为: .
的取值范围为: .
②若函数![]() 的图象与该函数有三个交点,则
的图象与该函数有三个交点,则![]() 的取值范围为: .
的取值范围为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:

(Ⅰ)图1中a的值为 ;
(Ⅱ)求统计的这组初赛成绩数据的平均数、众数和中位数;
(Ⅲ)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65m的运动员能否进入复赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级某班联欢会上,节目组设计了一个即兴表演节目游戏,在一个不透明的盒子里,放有五个完全相同的乒乓球,乒乓球上分别标有数字1,2,3,4,5,游戏规则是:参加联欢会的50名同学,每人同时从盒子里一次摸出两个乒乓球,若两球上数字之和是偶数就给大家即兴表演一个节目;否则,下一个同学依次进行,直至50名同学都模完,
(1)若小朱是该班同学,用列表法或画树状图法求小朱同学表演节目的概率
(2)若参加联欢会的同学每人都有一次摸球的机会,请估计本次联欢会上有多少个同学表演节目?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com