
【题目】如图,在ABCD中,E是AD上一点,连接BE,F为BE中点,且AF=BF, 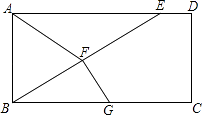
(1)求证:四边形ABCD为矩形;
(2)过点F作FG⊥BE,垂足为F,交BC于点G,若BE=BC,S△BFG=5,CD=4,求CG.
【答案】
(1)证明:∵F为BE中点,AF=BF,
∴AF=BF=EF,
∴∠BAF=∠ABF,∠FAE=∠AEF,
在△ABE中,∠BAF+∠ABF+∠FAE+∠AEF=180°,
∴∠BAF+∠FAE=90°,
又四边形ABCD为平行四边形,
∴四边形ABCD为矩形;
(2)解:连接EG,过点E作EH⊥BC,垂足为H,
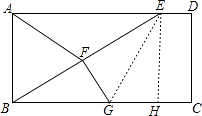
∵F为BE的中点,FG⊥BE,
∴BG=GE,
∵S△BFG=5,CD=4,
∴S△BGE=10= ![]() BGEH,
BGEH,
∴BG=GE=5,
在Rt△EGH中,GH= ![]() =3,
=3,
在Rt△BEH中,BE= ![]() =4
=4 ![]() =BC,
=BC,
∴CG=BC﹣BG=4 ![]() ﹣5
﹣5
【解析】(1)求出∠BAE=90°,根据矩形的判定推出即可;(2)求出△BGE面积,根据三角形面积公式求出BG,得出EG长度,根据勾股定理求出GH,求出BE,得出BC长度,即可求出答案.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对平行四边形的性质的理解,了解平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.


科目:初中数学 来源: 题型:
【题目】已知线段AB与x轴平行,点A坐标为(3,2),AB=4,则点B的坐标为( )
A.(7,2)B.(-1,2)或(7,2)C.(3,6)D.(3,6)或(3,-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】频数、频率与实验总次数之间的关系是 ( )
A. 频数越大,频率越大 B. 总次数一定时,频数越大,频率可无限大
C. 频数与总次数成正比 D. 频数一定时,频率与总次数成反比
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中.适合采取全面调查方式的是( )
A.了解某城市的空气质量的情况B.了解全国中学生的视力情况
C.了解某企业对应聘人员进行面试的情况D.了解某池塘中鱼的数量的情况
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列调查中,宜采用全面调查的是( )
A.了解某区中小学生视力情况B.了解老年人对预防新冠状病毒知识的掌握
C.了解一批灯泡的使用寿命D.了解某市百岁以上老人的健康情况
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人距B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题: 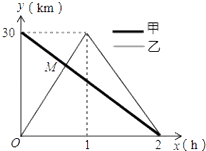
(1)写出A、B两地之间的距离;
(2)求出点M的坐标,并解释该点坐标所表示的实际意义;
(3)若两人之间保持的距离不超过3km时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,须用普查的是( )
A.了解我区初三同学的视力情况
B.了解我区初三同学课外阅读的情况
C.了解我区初三同学今年4月12日回校报到时的校园健康“入学码”情况
D.了解我区初三同学疫情期间参加晨练的情况
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com