
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 、
、![]() 、
、![]() 分别在
分别在![]() 、
、![]() 、
、![]() 边上,且
边上,且![]() ,
,![]() .
.

(1)求证:![]() 是等腰三角形;
是等腰三角形;
(2)当![]() 时,求
时,求![]() 的度数;
的度数;
(3)当![]() 为多少度时,
为多少度时,![]() ?请说明理由.
?请说明理由.
【答案】(1)见解析(2)65°;(3)40°.
【解析】
(1)根据AB=AC可得∠B=∠C,即可求证△BDE≌△CEF,即可解题;
(2)根据全等三角形的性质得到∠CEF=∠BDE,于是得到∠DEF=∠B,根据等腰三角形的性质即可得到结论;
(3)由(2)得∠DEF=∠B,根据三角形的内角和与等腰三角形的性质即可求解.
(1)∵AB=AC,
∴∠B=∠C,
在△BDE和△CEF中,
∵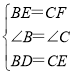 ,
,
∴△BDE≌△CEF(SAS),
∴DE=EF,
∴△DEF是等腰三角形;
(2)∵∠DEC=∠B+∠BDE,
即∠DEF+∠CEF=∠B+∠BDE,
∵△BDE≌△CEF,
∴∠CEF=∠BDE,
∴∠DEF=∠B,
又∵在△ABC中,AB=AC,∠A=50°,
∴∠B=65°,
∴∠DEF=65°;
(3)由(2)得∠DEF=∠B,
∵![]()
∴∠DEF=∠B=70°,
∴∠A=180°-2∠B=40°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,等边△OAB的顶点A在x轴的负半轴上,点B(a,b)在第二象限内,且a,b满足![]() .点P是y轴上的一个动点,以PA为边作等边△PAC,直线BC交x轴于点M,交y轴于点D.
.点P是y轴上的一个动点,以PA为边作等边△PAC,直线BC交x轴于点M,交y轴于点D.
(1)求点A的坐标;
(2)如图2,当点P在y轴正半轴上时,求点M的坐标;
(3)如图3,当点P在y轴负半轴上时,求出OP,CD,AD满足的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2-12ax+36a-5的图象在4<x<5这一段位于x轴下方,在8<x<9这一段位于x轴上方,则a的值为___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:对于两个不等的非零实数![]() 、
、![]() ,若分式
,若分式![]() 的值为零,则
的值为零,则![]() 或
或![]() .又因为
.又因为![]() ,所以关于
,所以关于![]() 的方程
的方程![]() 有两个解,分别为
有两个解,分别为![]() ,
,![]() .
.
应用上面的结论解答下列问题:
(1)方程![]() 的两个解分别为
的两个解分别为![]() ,
,![]() ,则
,则![]() _________,
_________,![]() _________;
_________;
(2)方程![]() 的两个解分别为
的两个解分别为![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)关于![]() 的方程
的方程![]() 的两个解分别为
的两个解分别为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个质点在第一象限及x轴、y轴上运动,且每秒移动一个单位,在第1秒钟,它从原点运动到(0,1),然后接着按图中箭头所示方向运动,即(0,0)→(0,1)→(1,1)→(1,0)→…,若经过23秒质点到达点A,经过33秒质点到达点B,则直线AB的解析式为( )

A.y=![]() x+
x+![]() B.y=﹣
B.y=﹣![]() x+
x+![]() C.y=2x+9D.y=﹣2x+9
C.y=2x+9D.y=﹣2x+9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,…,其中从第三个数起,每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的边长值构造正方形,再分别依次从左到右取2个、3个、4个、5个…正方形拼成如上长方形,若按此规律继续作长方形,则序号为⑦的长方形周长是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com