
分析 (1)由绝对值的非负性即可得出关于a、b的二元一次方程组,解之即可得出结论;
(2)找出运动时间为t秒时,点P、Q对应的数,利用两点间的距离公式即可得出PQ、PQ、PB的长度,结合|PA|+|PB|=2|PQ|即可得出关于t的含绝对值符号的一元一次方程,解之即可得出结论;
(3)假设存在,找出运动时间为t秒时,点A、C对应的数,根据两点间的距离公式找出|TA|、|TC|、|TB|、|TD|的值,分t<6.5、6.5≤t≤9和t>9三种情况考虑|TA|+|TC|+|TB|+|TD|的值,此题得解.
解答 解:(1)∵|a+3|+|b+3a|=0,
∴$\left\{\begin{array}{l}{a+3=0}\\{b+3a=0}\end{array}\right.$,
∴a=-3,b=9.
(2)当运动的时间为t秒时,P所对应的数为-3+3t,Q所对应的数为9-2t,
∴PQ=|-3+3t-(9-2t)|=|5t-12|,PA=3t,PB=|-3+3t-9|=|3t-12|.
∵|PA|+|PB|=2|PQ|,
∴3t+|3t-12|=2|5t-12|,
解得:t=1.2或t=3.6或t=3(舍去).
∴若|PA|+|PB|=2|PQ|,运动时间t为1.2秒或3.6秒.
(3)假设存在,当运动时间为t秒时,点A对应的数为2t-3,点C对应的数为2t-8,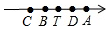
∵点B对应的是为9,点T对应的数为10,点D对应的数为11,
∴|TA|=|2t-3-10|=|2t-13|,|TC|=|2t-8-10|=|2t-18|,|TB|=|10-9|=1,|TD|=|10-11|=1,
∴|TA|+|TC|+|TB|+|TD|=|2t-13|+|2t-18|+2.
当2t-13<0,即t<6.5时,|TA|+|TC|+|TB|+|TD|=13-2t+18-2t+2=33-4t>33-26=7;
当0≤2t-13,2t-18≤0,即6.5≤t≤9时,|TA|+|TC|+|TB|+|TD|=2t-13+18-2t+2=7;
当2t-18>0,即t>9时,|TA|+|TC|+|TB|+|TD|=2t-13+2t-18+2=4t-29>36-29=7.
∴假设成立,
∴当6.5≤t≤9时,|TA|+|TC|+|TB|+|TD|取最小值7.
点评 本题考查了一元一次方程的应用、数轴、解二元一次方程组以及绝对值的非负性,解题的关键是:(1)根据绝对值的非负性找出关于a、b的二元一次方程组;(2)利用两点间的距离公式结合|PA|+|PB|=2|PQ|列出关于t的含绝对值符号的一元一次方程;(3)分t<6.5、6.5≤t≤9和t>9三种情况考虑.


科目:初中数学 来源: 题型:填空题
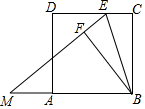 如图,E为正方形ABCD的边DC上一点,DE=2EC=2,将△BEC沿BE所在的直线对折得到△BEF,延长EF交BA的延长线于点M,则AM=2.
如图,E为正方形ABCD的边DC上一点,DE=2EC=2,将△BEC沿BE所在的直线对折得到△BEF,延长EF交BA的延长线于点M,则AM=2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{5}$:2 | B. | 4:5 | C. | 3:5 | D. | 10:25 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
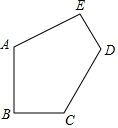 如图,已知AB=AE=$\sqrt{3}$,BC=DE=1,∠B=∠E=90°,∠A=120°,五边形ABCDE的面积是( )
如图,已知AB=AE=$\sqrt{3}$,BC=DE=1,∠B=∠E=90°,∠A=120°,五边形ABCDE的面积是( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | 8 | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,数轴上点A,B,C分别表示有理数a,b,c,若ac<0,a+b>0,则原点位于( )
如图,数轴上点A,B,C分别表示有理数a,b,c,若ac<0,a+b>0,则原点位于( )| A. | 点A的左侧 | B. | 点A与点B之间 | C. | 点B与点C之间 | D. | 在点C的右侧 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a-4>b-3 | B. | $-\frac{1}{2}a>-\frac{1}{2}b$ | C. | 1+2a>1+2b | D. | a2>b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com