
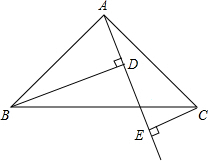
 如图,Rt△ABC中,AB=AC,∠BAC=90°,直线AE是经过点A的任一直线,BD⊥AE于D,CE⊥AE于E,若BD>CE,试问:
如图,Rt△ABC中,AB=AC,∠BAC=90°,直线AE是经过点A的任一直线,BD⊥AE于D,CE⊥AE于E,若BD>CE,试问:
|


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
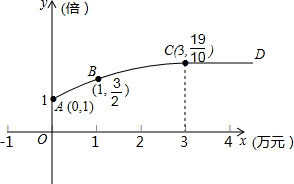 某公司生产一种产品,每件成本3元,售价4元,年销售量20万件,为获得更好的效益,公司准备拿出一定资金做广告.根据经验,设广告费x万元,做广告后的年销售量是原销售量的y倍,且y与x的关系如图所示,图中ABC为抛物线一段,CD为一条平行于x轴的射线,如果把利润看成是销售总额减去成本费和广告费
某公司生产一种产品,每件成本3元,售价4元,年销售量20万件,为获得更好的效益,公司准备拿出一定资金做广告.根据经验,设广告费x万元,做广告后的年销售量是原销售量的y倍,且y与x的关系如图所示,图中ABC为抛物线一段,CD为一条平行于x轴的射线,如果把利润看成是销售总额减去成本费和广告费查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com