
【题目】如图1,在△ABC中,∠B=60°,点M从点B出发沿射线BC方向,在射线BC上运动.在点M运动的过程中,连结AM,并以AM为边在射线BC上方,作等边△AMN,连结CN.

(1)当∠BAM= °时,AB=2BM;
(2)请添加一个条件: ,使得△ABC为等边三角形;
①如图1,当△ABC为等边三角形时,求证:CN+CM=AC;
②如图2,当点M运动到线段BC之外(即点M在线段BC的延长线上时),其它条件不变(△ABC仍为等边三角形),请写出此时线段CN、CM、AC满足的数量关系,并证明.
【答案】(1)30;(2)AB=AC;①证明见解析;②CN-CM=AC,理由见解析
【解析】
(1)根据含30°角的直角三角形的性质解答即可;
(2)利用含一个60°角的等腰三角形是等边三角形的判定解答;①利用等边三角形的性质和全等三角形的判定证明△BAM≌△CAN,从而利用全等三角形的性质求解;②利用等边三角形的性质和全等三角形的判定证明△BAM≌△CAN,从而利用全等三角形的性质求解.
解:(1)当∠BAM=30°时,
∴∠AMB=180°﹣60°﹣30°=90°,
∴AB=2BM;
故答案为:30;
(2)∵在△ABC中,∠B=60°
∴当AB=AC时,可得可得△ABC为等边三角形;
故答案为:AB=AC;
①如图1中,
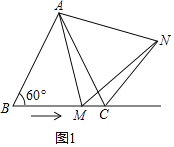
∵△ABC与△AMN是等边三角形,
∴AB=AC=BC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAC﹣∠MAC=∠MAN﹣∠MAC,
即∠BAM=∠CAN,
在△BAM与△CAN中,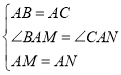 ,
,
∴△BAM≌△CAN(SAS),
∴BM=CN;
∴AC=BC=BM+CM=CM+CN
即CN+CM=AC;
②CN-CM=AC,
理由:如图2中,
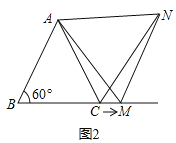
∵△ABC与△AMN是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAC+∠MAC=∠MAN+∠MAC,
即∠BAM=∠CAN,
在△BAM与△CAN中,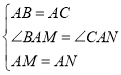 ,
,
∴△BAM≌△CAN(SAS),
∴BM=CN
∴AC=BC=BM-CM=CN-CM
即CN-CM=AC


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】为积极响应新旧动能转换.提高公司经济效益.某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为40万元时,年销售量为600台;每台售价为45万元时,年销售量为550台.假定该设备的年销售量y(单位:台)和销售单价![]() (单位:万元)成一次函数关系.
(单位:万元)成一次函数关系.
(1)求年销售量![]() 与销售单价
与销售单价![]() 的函数关系式;
的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于70万元,如果该公司想获得10000万元的年利润.则该设备的销售单价应是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,D为AB上一点,过D点作AB垂线,交AC于E,交BC的延长线于F.

(1)∠1与∠B有什么关系?说明理由.
(2)若BC=BD,请你探索AB与FB的数量关系,并且说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=EC.求证:

(1)△ABC≌△DEF;
(2)FG=CG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分)阅读材料:分解因式:![]()
解:![]()
=![]()
=![]()
=![]()
=![]()
=![]() ,
,
此种方法抓住了二次项和一次项的特点,然后加一项,使三项成为完全平方式,我们把这种分解因式的方法叫配方法.
(1)用上述方法分解因式:![]() ;
;
(2)无论![]() 取何值,代数式
取何值,代数式![]() 总有一个最小值,请尝试用配方法求出当
总有一个最小值,请尝试用配方法求出当![]() 取何值时代数式的值最小,并求出这个最小值.
取何值时代数式的值最小,并求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面一元二次方程的解法中,正确的是( )
A. (x-3)(x-5)=10×2,∴x-3=10,x-5=2,∴x1=13,x2=7
B. (2-5x)+(5x-2)2=0,∴(5x-2)(5x-3)=0,∴x1=![]() ,x2=
,x2=![]()
C. (x+2)2+4x=0,∴x1=2,x2=-2
D. x2=x 两边同除以x,得x=1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的网格中有四条线段AB、CD、EF、GH(线段端点在格点上),
⑴选取其中三条线段,使得这三条线段能围成一个直角三角形.
答:选取的三条线段为 .
⑵只变动其中两条线段的位置,在原图中画出一个满足上题的直角三角形(顶点仍在格点,并标上必要的字母).
答:画出的直角三角形为△ .
⑶所画直角三角形的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
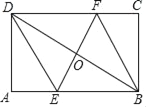
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB、CD边于点E、F.
(1)求证:四边形BEDF是平行四边形;
(2)求证:△ADE≌△CBF;
(3)当四边形BEDF是菱形时,直接写出线段EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com