
【题目】如图,在平面直角坐标系中,直线 ![]() 与抛物线
与抛物线 ![]() 交于A、B两点,点A在x轴上,点B的横坐标为-8.
交于A、B两点,点A在x轴上,点B的横坐标为-8.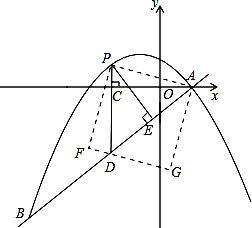
(1)求该抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为C,交直线AB于点D,作PE⊥AB于点E.
①设△PDE的周长为 ![]() ,点P的横坐标为
,点P的横坐标为 ![]() ,求
,求 ![]() 关于
关于 ![]() 的函数关系式,并求出
的函数关系式,并求出 ![]() 的最大值;
的最大值;
②连接PA,以PA为边作图示一侧的正方形APFG.随着点P的运动,正方形的大小、位置也随之改变.当顶点F或G恰好落在 ![]() 轴上时,求出对应点P的坐标.
轴上时,求出对应点P的坐标.
【答案】
(1)解:对于 ![]() ,当y=0,x=2.当x=-8时,y=-
,当y=0,x=2.当x=-8时,y=- ![]() .
.
∴A点坐标为(2,0),B点坐标为(-8,- ![]() ).
).
由抛物线 ![]() 经过A、B两点,得
经过A、B两点,得 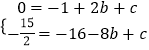 ,解得
,解得 ![]() ,
, ![]() .
.
∴ ![]() ;
;
(2)解:①设直线 ![]() 与y轴交于点M,
与y轴交于点M,
当x=0时,y= ![]() .∴OM=
.∴OM= ![]() .
.
∵点A的坐标为(2,0),∴OA=2.
∴AM= ![]() .
.
∴OM∶OA∶AM=3∶4∶5.
由题意得,∠PDE=∠OMA,∠AOM=∠PED=90°,
∴△AOM∽△PED.
∴DE∶PE∶PD=3∶4∶5.
∵点P是直线AB上方的抛物线上一动点,
∵PD⊥x轴,
∴PD两点横坐标相同,
∴PD=yP-yD= ![]() =
= ![]() ,
,
∴ ![]() .
.
∴x=-3时,l最大=15;

②当点G落在y轴上时,如图2,
由△ACP≌△GOA得PC=AO=2,
即 ![]() ,解得x=
,解得x= ![]() ,
,
所以P1( ![]() ,2),P2(
,2),P2( ![]() ,2),
,2),
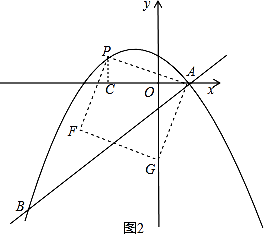
如图3,过点P作PN⊥y轴于点N,过点P作PS⊥x轴于点S,
由△PNF≌△PSA,
PN=PS,可得P点横纵坐标相等,
故得当点F落在y轴上时, ![]() ,解得
,解得 ![]() ,
,
可得P3( ![]() ,
, ![]() ),
),
P4( ![]() ,
, ![]() ),(舍去).
),(舍去).
综上所述:满足题意的点P有三个,分别是P1( ![]() ,2),P2(
,2),P2( ![]() ,2),P3(
,2),P3( ![]() ,
, ![]() ).
).
【解析】(1)利用一次函数的解析式当y=0时求出点A的坐标,再将x=-8代入函数解析式求出B的坐标,再利用待定系数法求二次函数解析式解答。
(2)①设z直线AB与y轴交于点M,根据勾股定理求出AM长,及三边之比,再证明△AOM∽△PED.得出DE∶PE∶PD=3∶4∶5,由点P是直线AB上方的抛物线上一动点,PD⊥x轴,得出P、D两点横坐标相同,即可求出PD的长,再根据三角形的周长公式列式整理即可得解,再根据二次函数的最值问题解答。
②当点G在y轴上时,根据正方形的性质,先证△ACP≌△GOA,得PC=AO=2,根据二次函数的解析式建立方程求解,即可求出点P的坐标;
当点F在y轴上时,过点PM⊥x轴于M,作PN⊥y轴于N,根据正方形的性质,先证△PNF≌△PSA,得出PN=PS,可得P点横纵坐标相等,建立方程求解,即可求出点P的坐标。
【考点精析】利用二次函数的最值和正方形的性质对题目进行判断即可得到答案,需要熟知如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】如图,△ACE是以ABCD的对角线AC为边的等边三角形,点C与点E关于x轴对称.若E点的坐标是(7,﹣3![]() ),则D点的坐标为( )
),则D点的坐标为( )

A. (3,0)
B. (4,0)
C. (5,0)
D. (6,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
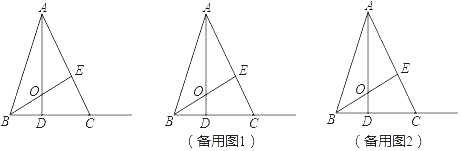
【题目】如图,在△ABC中,BC=5,高AD、BE相交于点O,BD=![]() CD,且AE=BE.
CD,且AE=BE.
(1)求线段AO的长;
(2)动点P从点O出发,沿线段OA以每秒1个单位长度的速度向终点A运动,动点Q从点B出发沿射线BC以每秒4个单位长度的速度运动,P、Q两点同时出发,当点P到达A点时,P、Q两点同时停止运动.设点P的运动时间为t秒,△POQ的面积为S,请用含t的式子表示S,并直接写出相应的t的取值范围;
(3)在(2)的条件下,点F是直线AC上的一点且CF=BO.是否存在t值,使以点B、O、P为顶点的三角形与以点F、C、Q为顶点的三角形全等?若存在,请直接写出符合条件的t值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
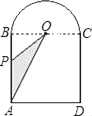
【题目】如图是一个由正方形ABCD和半圆O组成的封闭图形,点O是圆心.点P从点A出发,沿线段AB,弧BC和线段CD匀速运动,到达终点D.运动过程中OP扫过的面积(s)随时间(t)变化的图象大致是( )
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知用3辆A型车和2辆B型车一次可运货19吨;用2辆A型车和3辆B型车一次可运货 21吨.(每辆车每次都满载货物)
(1)求1辆A型车和1辆B型车载满货物一次分别可以运多少吨?
(2)某货物中心现有49吨货物,计划同时租用A型车和B型车若干辆,一次运完,且恰好每辆车都载满货物,请问有哪几种不同的租车方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店用8000元购进一批衬衫,以58元/件的价格出售,很快售完,然后又用17600元购进同款衬衫,购进数量是第一次的2倍,购进的单价比上一次每件多4元,服装店仍按原售价58元/件出售,并且全部售完.
(1)该服装店第一次购进衬衫多少件?
(2)将该服装店两次购进衬衫看作一笔生意,那么这笔生意是盈利还是亏损?求出盈利(或亏损)多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后解答后面的问题.
我们知道方程2x+3y=12有无数组解,但在实际生活中我们往往只需要求出其正整数解.例:由2x+3y=12,得![]() ,(x、y为正整数)∴
,(x、y为正整数)∴![]() 则有0<x<6.又
则有0<x<6.又![]() 为正整数,则
为正整数,则![]() 为正整数.
为正整数.
由2与3互质,可知:x为3的倍数,从而x=3,代入![]() .
.
∴2x+3y=12的正整数解为![]()
问题:
(1)请你写出方程2x+y=5的一组正整数解:______;
(2)若![]() 为自然数,则满足条件的x值有______个;
为自然数,则满足条件的x值有______个;
A、2B、3C、4D、5
(3)七年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的面积为20cm2,对角线交于点O;以AB、AO为邻边做平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边做平行四边形AO1C2B;…依此类推,则平行四边形AO4C5B的面积为( )

A. ![]() cm2 B.
cm2 B. ![]() cm2 C.
cm2 C. ![]() cm2 D.
cm2 D. ![]() cm2
cm2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com