
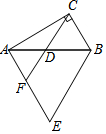
 如图,在△ABC中,∠ACB=90°,∠CBA=60°.△ABE是等边三角形,D是AB的中点,连接CD并延长,交AE于点F.若CD=2,则EF的长为( )
如图,在△ABC中,∠ACB=90°,∠CBA=60°.△ABE是等边三角形,D是AB的中点,连接CD并延长,交AE于点F.若CD=2,则EF的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | $\frac{3}{2}$ |
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:选择题
| A. | ma<mb | B. | 2a>2b | C. | -2a>-2b | D. | $\frac{a}{2}$>$\frac{b}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
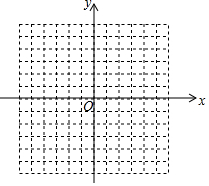 如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点(即这些小正方形的顶点)上,且它们的坐标分别是A(2,-3),B(5,-1),C(-1,3),结合所给的平面直角坐标系,解答下列问题:
如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点(即这些小正方形的顶点)上,且它们的坐标分别是A(2,-3),B(5,-1),C(-1,3),结合所给的平面直角坐标系,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
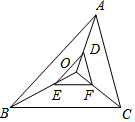 如图,在O为△ABC内一点,D,E,F分别是OA,OB,OC上的点,且$\frac{OD}{AD}$=$\frac{OE}{BE}$=$\frac{OF}{CF}$=$\frac{1}{2}$,则$\frac{EF}{BC}$=( )
如图,在O为△ABC内一点,D,E,F分别是OA,OB,OC上的点,且$\frac{OD}{AD}$=$\frac{OE}{BE}$=$\frac{OF}{CF}$=$\frac{1}{2}$,则$\frac{EF}{BC}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
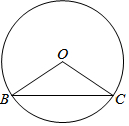 在⊙O中,己知弦BC所对的圆周角∠BAC与圆心角∠BOC互补.
在⊙O中,己知弦BC所对的圆周角∠BAC与圆心角∠BOC互补.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com