
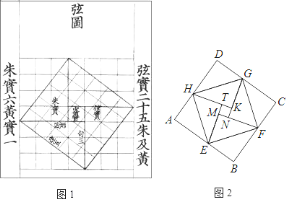
【题目】我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图![]() ),图
),图![]() 由弦图变化得到,它是由作个全等的直角三角形拼接而成,记图中正方形
由弦图变化得到,它是由作个全等的直角三角形拼接而成,记图中正方形![]() ,正方形
,正方形![]() ,正方形
,正方形![]() 的面积分别为
的面积分别为![]() 、
、![]() 、
、![]() ,若
,若![]() ,则
,则![]() 的值是( )
的值是( )
A. 5 B. ![]() C.
C. ![]() D. 4
D. 4
 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边为a,较长直角边为b,那么(a+b)2的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,BD=CF,BE=CD,∠EDF=a,则下列结论正确的是( )
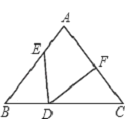
A. a+∠A=90° B. a+∠A=180° C. 2a+∠A=90° D. 2a+∠A=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG,EF与AD相交于点H,延长DA交GF于点K.若正方形ABCD边长为 ![]() ,则AK= .
,则AK= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+bx+c与x轴交于A(2,0),B(﹣4,0)两点.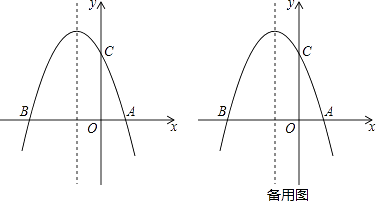
(1)求该抛物线的解析式;
(2)若抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
(3)在抛物线的第二象限图象上是否存在一点P,使得△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若不存,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=BC.延长DA与⊙O的另一个交点为E,连接AC,CE. 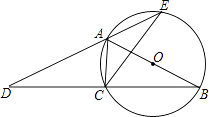
(1)求证:∠B=∠D;
(2)若AB=13,BC﹣AC=7,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若A的对应点A2的坐标为(0,4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com