
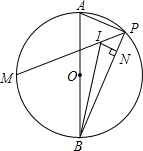
 如图,AB为⊙O的直径,点M为半圆的中点,点P为另一半圆上一点(不与A、B重合),点I为△ABP的内心,IN⊥BP于N.
如图,AB为⊙O的直径,点M为半圆的中点,点P为另一半圆上一点(不与A、B重合),点I为△ABP的内心,IN⊥BP于N.分析 (1)连接OM.根据“同弧所对的圆周角是所对的圆心角的一半”进行解答,即可证得结论;
(2)连接AM、BM.根据三角形PIB的外角定理、三角形的内心的定义证得△MBI的两边MB=IM;根据勾股定理求得AB=$\sqrt{2}$MB.易证该结论;
(3)根据直角三角形内切圆半径公式、圆的半径与直径是数量关系求得IN+OB=$\frac{1}{2}$(AP+BP);然后过点A作AG⊥PM于点G,过点B作BH⊥PM于点H,连接AM,BM,易得△APG与△BPH是等腰直角三角形且△AMG≌△MBH,继而求得AP+BP=$\sqrt{2}$(PH+MH)=$\sqrt{2}$PM,继而求得答案.
解答 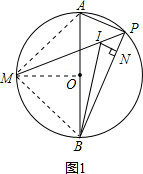 (1)证明:如图1,连接OM.
(1)证明:如图1,连接OM.
∵点M是半圆的中点,
∴∠AOM=90°.
∵∠APM=$\frac{1}{2}$∠AOM,
∴∠APM=45°;
(2)证明:如图1,连接AM、BM.
∵点M是半圆的中点,
∴$\widehat{AM}$=$\widehat{BM}$,
∴AM=BM,
∵∠AOM=90°,
∴AB=$\sqrt{2}$MB.
∵∠ABM=$\frac{1}{2}$AOM=45°,∠BPI=$\frac{1}{2}$∠BOM=45°,
∴∠ABM=∠BPI,
∵点I为△ABP的内心,
∴∠ABI=∠PBI,
∵∠MIB=∠BPI+∠PBI,∠MBI=∠ABM+∠ABI,
∴∠MIB=∠MBI,
∴MB=IM.
∴AB=$\sqrt{2}$IM;
(3)不变.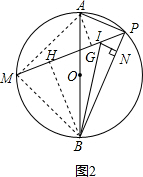 理由:
理由:
解:根据直角三角形内切圆半径公式知,IN=$\frac{AP+BP-AB}{2}$,则IN+OB=$\frac{1}{2}$(AP+BP),
如图2,过点A作AG⊥PM于点G,过点B作BH⊥PM于点H,连接AM,BM,
则△APG与△BPH是等腰直角三角形,∠AGM=∠MHB=90°,
∴PB=$\sqrt{2}$PH,PA=$\sqrt{2}$AG,
∵∠AMG+∠BMH=∠AMG+∠MAG=90°,
∴∠MAG=∠BMH,
在△AMG和△MBH中,
$\left\{\begin{array}{l}{∠AGM=∠MHB}\\{∠MAG=∠BMH}\\{AM=MB}\end{array}\right.$,
∴△AMG≌△MBH(AAS),
∴AG=MH,
∴PA=$\sqrt{2}$MH,
∴AP+BP=$\sqrt{2}$(PH+MH)=$\sqrt{2}$PM,
∴$\frac{IN+OB}{PM}$=$\frac{\sqrt{2}}{2}$.
点评 本题考查了圆的综合题.本题涉及到的知识点有:圆周角定理,直角三角形的内切圆半径公式,三角形的内切圆的性质以及等腰三角形的判定与性质等知识.注意准确作出辅助线是解此题的关键.


科目:初中数学 来源: 题型:解答题
 如图,有A、B两个转盘,其中转盘A被分成4等份,转盘B被分成3等份,并在每一份内标上数字.现甲、乙两人同时分别转动其中一个转盘,转盘停止后(当指针指在边界线上时视为无效,重转),若将A转盘指针指向的数字记为x,B转盘指针指向的数字记为y,从而确定点P的坐标为P(x,y).
如图,有A、B两个转盘,其中转盘A被分成4等份,转盘B被分成3等份,并在每一份内标上数字.现甲、乙两人同时分别转动其中一个转盘,转盘停止后(当指针指在边界线上时视为无效,重转),若将A转盘指针指向的数字记为x,B转盘指针指向的数字记为y,从而确定点P的坐标为P(x,y).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知AB=14,C、D是线段AB上的两个点,且满足AC:CD:DB=1:2:4,点M是线段AC的中点.
如图,已知AB=14,C、D是线段AB上的两个点,且满足AC:CD:DB=1:2:4,点M是线段AC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知∠AOB与∠BOC的和为180°,OD是∠AOB的平分线,OE在∠BOC内,∠BOE=$\frac{1}{2}$∠EOC,∠DOE=72°,求∠EOC及∠DOC的度数.
如图,已知∠AOB与∠BOC的和为180°,OD是∠AOB的平分线,OE在∠BOC内,∠BOE=$\frac{1}{2}$∠EOC,∠DOE=72°,求∠EOC及∠DOC的度数.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABC是边长为5的等边三角形,△BDC是等腰三角形,且∠BDC=120°.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为10.
如图,△ABC是边长为5的等边三角形,△BDC是等腰三角形,且∠BDC=120°.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为10.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,把一张矩形纸片ABCD沿EF折叠后,点C,D分别落在C′,D′的位置上,EC′交AD于点G.已知∠EFG=58°,那么∠FEG=( )
如图,把一张矩形纸片ABCD沿EF折叠后,点C,D分别落在C′,D′的位置上,EC′交AD于点G.已知∠EFG=58°,那么∠FEG=( )| A. | 58° | B. | 60° | C. | 45° | D. | 30° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com